Домашнее задание. 1. Найти координаты вектора , заданного в базисе в новом базисе , если .

1. Найти координаты вектора 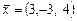, заданного в базисе в новом базисе , если .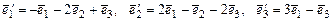

2. Найти координаты матрицы в стандартном базисе 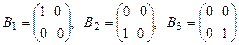и с помощью закона преобразования координат в базисе линейного пространства .

3. С помощью теоремы Кронекера-Капелли исследовать совместность следующих линейных систем:

3.1. ; 3.2. .

Фдз 3. Однородные и неоднородные системы линейных уравнений. Структура общего решения однородной системы, фундаментальная система решений. Структура общего решения неоднородной системы.

1. Сформулировать теорему о структуре общего решения линейной однородной системы.

2. Дать определение фундаментальной системы решений (ФСР).

3. Найти общее решение и ФСР однородной системы .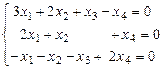

4. Найти общее решение и ФСР однородной системы .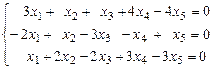

5. Найти общее решение и ФСР однородной системы .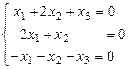

6. Сформулировать теорему о структуре общего решения совместной линейной неоднородной системы.

7. Найти общее решение неоднородной системы 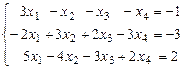и выделить из него общее решение соответствующей однородной системы и ее ФСР.

8. Найти общее решение неоднородной системы 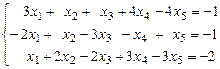и выделить из него общее решение соответствующей однородной системы и ее ФСР.

____________________________________________________________________