Фдз 1. Линейные пространства.
Повторение основных понятий и терминов, связанных с линейными пространствами (линейная зависимость, независимость системы векторов; базис и размерность линейного пространства; разложение вектора по базису; линейная оболочка системы векторов).
1. Дать определение линейного пространства.
2. Доказать, что множество 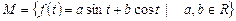 является линейным пространством.
является линейным пространством.
3. Дать определение линейной зависимости (независимости) системы векторов.
4. Доказать линейную зависимость системы векторов  из линейного пространства
из линейного пространства 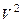 .
.
5. Доказать линейную независимость системы векторов 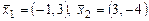 из линейного пространства
из линейного пространства 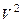 .
.
6. Доказать линейную независимость функций 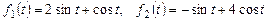 из линейного пространства
из линейного пространства 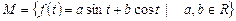 .
.
7. Разложить вектор 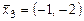 по векторам
по векторам 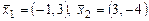 .
.
8. Дать определение полной системы векторов в линейном пространстве.
9. Доказать, что системы векторов
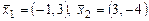 и
и  являются полными в
являются полными в 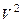 .
.
10. Дать первое и второе определение базиса линейного пространства.
11. Доказать, что система 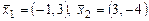 удовлетворяет и первому и второму определению базиса.
удовлетворяет и первому и второму определению базиса.
12. Доказать, что 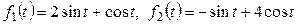 является базисом пространства
является базисом пространства 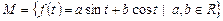 .
.
13. Дать определение линейного подпространства. Сформулировать критерий линейного подпространства.
14. Доказать, что множество 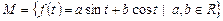 является подпространством пространства
является подпространством пространства 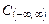 всех непрерывных на интервале
всех непрерывных на интервале 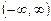 функций.
функций.
15. Дать определение линейной оболочки.
16. Линейной оболочкой каких функций является множество 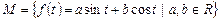 .
.
Дата добавления: 2015-07-30; просмотров: 780;
