Двойной интеграл и его свойства
Если интегральная сумма

при  имеет предел, равный числу
имеет предел, равный числу  то этот предел называется двойным интегралом от функции
то этот предел называется двойным интегралом от функции  по области
по области 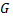 и обозначается
и обозначается
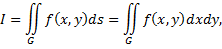
где функция  называется интегрируемой в области
называется интегрируемой в области  область интегрирования,
область интегрирования,  переменные интегрирования,
переменные интегрирования, 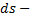 элемент площади. В данном случае предполагается, что
элемент площади. В данном случае предполагается, что  ограничена, что является необходимым условием интегрируемости.
ограничена, что является необходимым условием интегрируемости.
Для нахождения достаточных условий интегрируемости, как и в случае с одной переменной, удобно воспользоваться теорией сумм, которая полностью переносится на случай двойного интеграла.
Функция 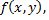 непрерывная в замкнутой ограниченной области
непрерывная в замкнутой ограниченной области 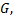 интегрируема в этой области.
интегрируема в этой области.
Не следует считать, что двойной интеграл существует только для непрерывных функций.
Функция 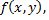 ограниченная в замкнутой ограниченной области
ограниченная в замкнутой ограниченной области 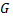 и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непрерывных функций
и непрерывная в ней всюду, кроме точек, лежащих на конечном числе кривых, являющихся графиками непрерывных функций 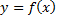 или
или 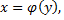 интегрируема в этой области.
интегрируема в этой области.
Основные свойства двойного интеграла аналогичны соответствующим свойствам определенного интеграла.
1)Если  произвольное число и функция
произвольное число и функция  интегрируема в области
интегрируема в области 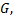 то функция
то функция  тоже интегрируема в области
тоже интегрируема в области 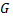

т.е. постоянный множитель можно выносить за знак интеграла.
2)Если функции  и
и 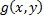 интегрируемы в области
интегрируемы в области 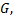 то их алгебраическая сумма также интегрируема в этой области
то их алгебраическая сумма также интегрируема в этой области 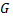

3)Если область 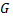 является объединением областей
является объединением областей  и
и 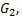 не имеющих общих точек, в каждой из которых функция
не имеющих общих точек, в каждой из которых функция  интегрируема, то в области
интегрируема, то в области 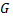 эта функция также интегрируема
эта функция также интегрируема

4)Если функция 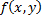 непрерывна в области
непрерывна в области 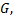 то в этой области найдется такая точка
то в этой области найдется такая точка  что
что
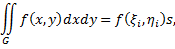
где  площадь фигуры
площадь фигуры 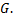
Дата добавления: 2015-08-11; просмотров: 1133;
