Определение криволинейного интеграла

Обобщим понятие определенного интеграла на случай, когда областью интегрирования является дуга некоторой кривой, лежащей в плоскости. Интегралы такого рода называются криволинейными. Они имеют широкое применение в различных разделах математики. Различают два типа криволинейных интегралов: криволинейные интегралы первого и второго рода.

Определение криволинейного интеграла первого рода. Рассмотрим на плоскости 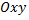некоторую кривую 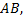гладкую или кусочно-гладкую, и предположим, что функция 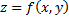определена и ограничена на кривой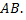

Разобьем кривую 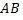произвольно на частей точками

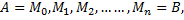
выберем на каждой из частичных дуг 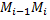произвольную точку 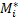и составим сумму

где 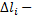длина дуги 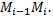Данная сумма называется интегральной суммой для функции 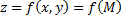по кривой 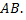Обозначим через наибольшую из длин частичных дуг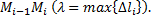

Если интегральная сумма при имеет предел, равный то этот предел называется криволинейным интегралом первого рода от функции по кривой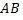

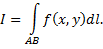
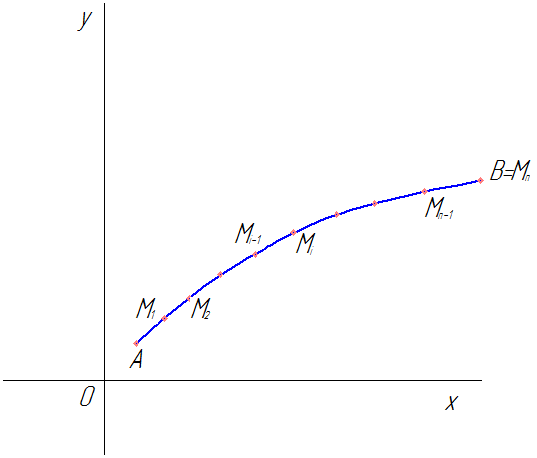
Рис. 58

Контур интегрирования

В этом случае функция называется интегрируемой вдоль кривой 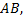кривая 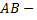контуром интегрирования, начальной, а 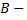конечной точками интегрирования.

Криволинейный интеграл первого рода сводится к определенному интегралу. Приняв на кривой 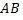за параметр длину дуги 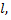отсчитываемую от точки 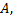получим параметрическое представление кривой

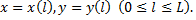
Тогда функция 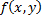, заданная вдоль 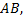становится сложной функцией параметра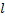

Таким образом, криволинейный интеграл выражается через определенный интеграл

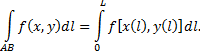
Криволинейный интеграл обладает всеми свойствами определенного интеграла за исключением одного, в интегральной сумме

величины 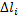обязательно положительны, независимо от того, какую точку кривой 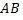считать начальной, а какую конечной, в то время как определенный интеграл

при перестановке пределов интегрирования меняет знак.

Криволинейный интеграл первого рода, так же как и определенный, имеет геометрический смысл. Если определенный интеграл

представляет собой площадь криволинейной трапеции, то криволинейный интеграл

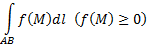
численно равен площади куска цилиндрической поверхности, которая составлена из перпендикуляров к плоскости восстановленных в точках 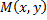кривой 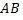и имеющих переменную длину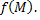

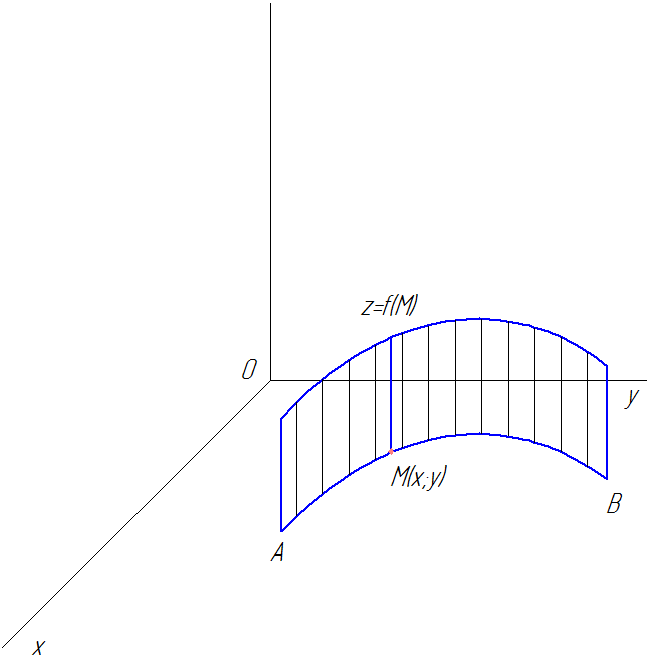
Рис. 59

Кусок цилиндрической поверхности

Если 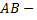не кривая, а отрезок прямой, расположенный на оси 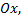то криволинейный интеграл будет обычным определенным интегралом.

Таким образом, с помощью криволинейного интеграла первого рода можно вычислять площадь цилиндрических поверхностей и длины дуг. Кроме того, с помощью криволинейного интеграла можно находить массу материальной кривой по ее плотности, моменты инерции относительно координатных осей, координаты центра масс такой кривой.

Криволинейный интеграл второго рода.

Пусть на кривой 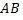определены две ограниченные функци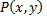и и 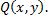Разобьем кривую 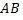на частей точками

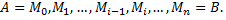
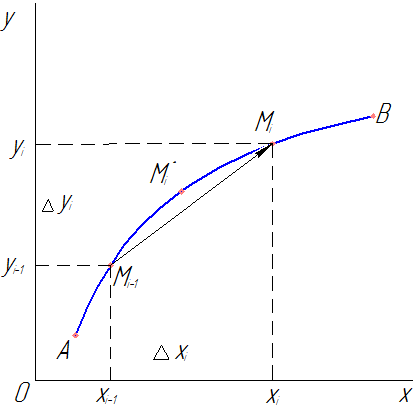
Рис. 60

Кривая АВ

Обозначим через 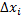и 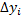проекции вектора 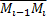на оси координат, на каждой частичной дуге 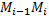возьмем произвольную точку 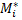и составим интегральную сумму для функции

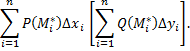
Если данная интегральная сумма при 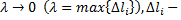длина дуги 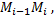имеет предел, равный то этот предел называется криволинейным интегралом второго рода от функции по кривой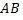

Сумму

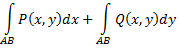
называют общим криволинейным интегралом второго рода

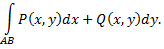
Криволинейные интегралы второго рода, как и интегралы первого рода, сводятся к определенным интегралам.

Пусть кривая 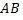задана параметрически уравнениями

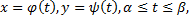
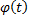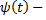где и непрерывные вместе со своими производным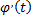и и 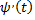функции, причем точке кривой соответствует значени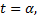е точке 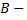значение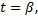

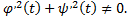
Пусть функци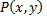и и 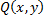непрерывны вдоль кривой 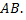Тогда справедливы формулы

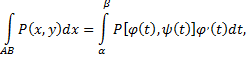
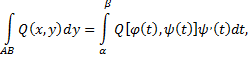
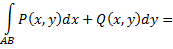
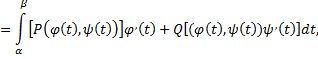
сводящие криволинейные интегралы к определенным интегралам.

Криволинейный интеграл второго рода обладает свойствами, аналогичными свойствам определенного интеграла. В отличие от криволинейного интеграла первого рода криволинейный интеграл второго рода зависит от того, в каком направлении проходится кривая 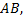и меняет знак при изменении направления обхода кривой, т.е.

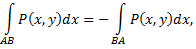
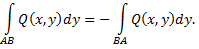
Таким образом, при вычислении криволинейных интегралов второго рода необходимо учитывать направление интегрирования.

В случае, когда замкнутая кривая, т.е. когда точка 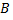совпадает с точкой 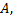из двух возможных направлений обхода замкнутого контура 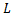называют положительным то направление, при котором область, лежащая внутри этого контура, остается слева по отношению к точке, совершающей обход. Противоположное направление обхода контура называют отрицательным.