Комплексные числа и их изображение на плоскости
Комплексные числа возникли в связи с задачей решения квадратных уравнений. Оставаясь в множестве действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексные числа необходимы в различных приложениях математики. В частности, теория функций комплексной переменной является действенным инструментом при использовании математических методов в различных областях науки.
Комплексным числом называется выражение вида 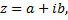 где
где  -действительные числа, -мнимая единица.
-действительные числа, -мнимая единица.
Итак, комплексным числом называется всякая упорядоченная пара 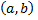 действительных чисел
действительных чисел  и
и  Действительное число
Действительное число  называют абсциссой комплексного числа
называют абсциссой комплексного числа 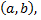 действительное число
действительное число  его ординатой
его ординатой

или
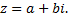
Всякое комплексное число можно изобразить на плоскости 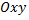 в виде точки
в виде точки 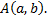 Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменного
Плоскость, на которой изображаются комплексные числа, называется плоскостью комплексного переменного 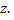
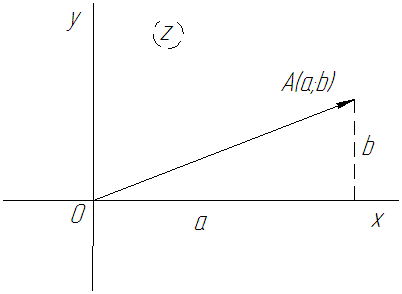
Рис. 62
Плоскость комплексного переменного
Действительные числа изображаются точками оси абсцисс, мнимые числа изображаются точками оси ординат. Поэтому ось 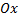 называют действительной осью, а ось ординат
называют действительной осью, а ось ординат  мнимой осью.
мнимой осью.
Соединив точку 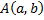 с началом координат, получим вектор
с началом координат, получим вектор  В некоторых случаях удобно считать геометрическим изображением комплексного числа
В некоторых случаях удобно считать геометрическим изображением комплексного числа 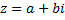 вектор
вектор 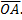 При этом действительная и мнимая части числа являются проекциями вектора
При этом действительная и мнимая части числа являются проекциями вектора  на действительную и мнимую оси.
на действительную и мнимую оси.
Обозначим через 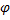 и
и 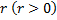 полярные координаты точки
полярные координаты точки  считая начало координат полюсом, а положительное направление оси
считая начало координат полюсом, а положительное направление оси 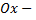 полярной осью.
полярной осью.
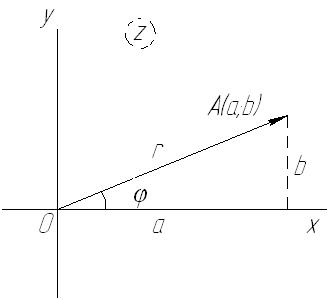
Рис. 63
Геометрическое изображение комплексного числа
Тогда имеют место следующие равенства
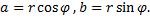
Следовательно, комплексное число 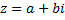 можно представить в виде
можно представить в виде

– это есть тригонометрическая форма записи комплексного числа  называется модулем комплексного числа
называется модулем комплексного числа  аргументом комплексного числа
аргументом комплексного числа 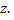
Дата добавления: 2015-08-11; просмотров: 2987;
