Модуль и аргумент комплексного числа

Обозначение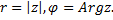

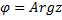определяется с точностью до слагаемого

Модуль и аргумент находятся следующим образом

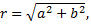
так как

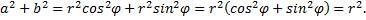
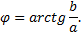
Так как

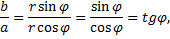
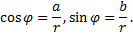
Пусть

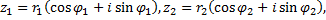
найдем произведение этих чисел:

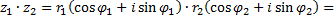
Произведение двух комплексных чисел есть такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент равен сумме аргументов сомножителей.

Найдем частное двух комплексных чисел

Модуль частного двух комплексных чисел равен частному модулей делимого и делителя, аргумент частного равен разности аргументов делимого и делителя.

Аргумент комплексного числа считается положительным, если он отсчитывается от положительного направления оси 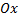против часовой стрелки, и отрицательным, если он отсчитывается по часовой стрелке. Аргумент 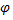определяется неоднозначно, а с точностью до слагаемого любое целое число.