J-модульована спінова луна.
Одним з найпростіших підходів до редагування спектрів є імпульсна послідовність J-модульованої спінової луни (Рис. 4.51а іноді називають SEFT – Spin-Echo Fourier Transform).



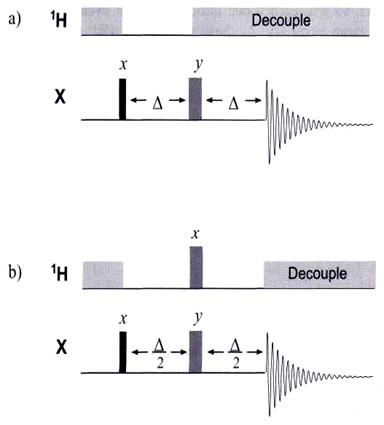
Рис. 4.51. Послідовність J-модульованої спін-луни, (a) варіант із переривчастим декаплінгом і (б) імпульсний варіант
Послідовність включає елемент спінової луни по каналу атомів вуглецю та постійний декаплінг по каналу протонів, який вимикається лише на час першого з двох однакових інтервалів D спінової луни. Її дію легко зрозуміти за допомогою векторної моделі. Ключем до розуміння дії послідовності є усвідомлення того, що еволюція векторів намагніченості ядер вуглецю під впливом гетероядерного розщеплення 1JCH відбувається тільки при вимкненому декаплері. Коли декаплер ввімкнений, спін-спінова взаємодія миттєво зникає, всі вектори намагніченості, що зумовлені гетероядерною ССВ об’єднаються в один сигнал по правилам векторного додавання і еволюціонують тільки вектори хімічних зсувів. Модель ще спрощується, якщо згадати про те, що можна повністю ігнорувати різницю в хімічних зсувах вуглецю, оскільки їхня еволюція під час першого інтервалу D повністю рефокусується під час другого інтервалу D, який міститься за 180о імпульсом. Тому при розгляді процесів, що відбуваються при дії послідовності, слід враховувати тільки наявність гетероядерного розщеплення під час першого періоду D. Для випадку, коли D змінюється від 0 до 1/J с. еволюція вектора намагніченості для різних мультиплетів показана на Рис. 4.52.
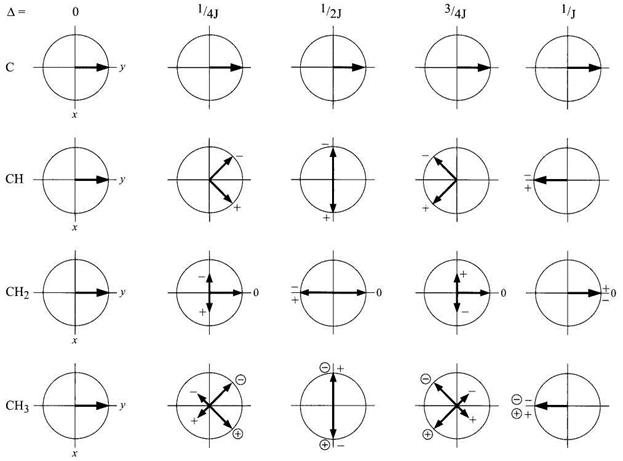
Рис. 4.52. еволюція векторів намагніченості вуглецю під впливом протон-вуглецевого спінового зв'язку
Таким чином, наприкінці періоду D вектори намагніченості, що відповідають різним гетероядерним мультиплетам, матимуть різну орієнтацію. При вмиканні в цей момент декаплера гетероядерне розщеплення зникне, але інтенсивність вуглецевого сигналу, що з’явиться в кінцевому спектрі, буде визначатися взаємною орієнтацією векторів намагніченості в момент включення декаплера. Інтенсивність сигналу визначатиметься векторною сумою компонентів намагніченості гетероядерних мультиплетів. Тобто, мультиплетність сигналів виявиться закодованою в їхній інтенсивності. Оскільки хімічні зсуви не відіграють ролі, то всі вуглецеві атоми, що зв’язані з певним числом протонів, будуть вести себе цілком однаково. Вектори намагніченості четвертинних атомів вуглецю не змінюються при дії імпульсної послідовності, оскільки вони не мають гетероядерного розщеплення сигналів і розташовані під час періоду D уздовж осі +у (далекі С-Н константи хоча й можуть бути присутніми, але їхня величина є значно меншою від прямих КССВ і ними можна знехтувати). Для пари спінів метинової групи СН є два вектори, що еволюціонують зі швидкістю +J/2 Гц. Тому кожний з них повертається на половину оберту за 1/J с. При цьому вони зустрічаються на осі -у. У цей момент вони на 180о відрізняються за фазою від векторів намагніченості четвертинних атомів вуглецю. У кінцевому спектрі сигнал такої групи буде інвертованим. Аналогічні міркування для сигналів з іншою мультиплетністю показують, що вектори намагніченості для метиленової групи, які обертаються зі швидкістю +J Гц у цей момент будуть орієнтованими уздовж осі +у, а вектори метильних груп, що обертаються з частотами +J/2 Гц і +3J/2 Гц, - уздовж осі -у. У більш загальному випадку при виборі кута q таким, щоб q=180JD (градусів), інтенсивності сигналів вуглецевих мультиплетів, I, змінюються відповідно до рівнянь:
С: I=I
CH: І = ICos q
CH2: І = Icos2 q
CH3: І = Icos3 q
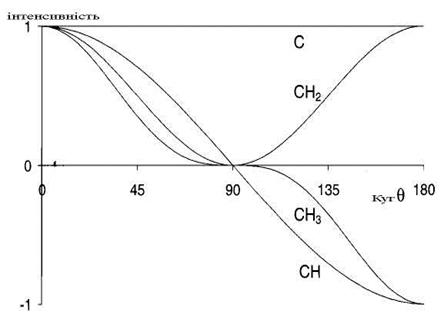
Рис.4.53. Зміна інтенсивності сигналів вуглецю в експерименті по J-модульованій спін-луні як функція періоду еволюції (q= 180JDо).
Ці рівняння можна подати в графічному вигляді. Їм відповідають графіки, що наведені на Рис. 4.53. Таким чином, маємо ситуацію, коли інтенсивність вуглецевих сигналів та їхній знак залежать від періоду D в імпульсній послідовності. Для кожного вибраного періоду D є своє співвідношення меж інтенсивностями вуглецевих сигналів. Для редагування спектру доцільно вибрати таке D, щоб різниця у співвідношеннях інтенсивностей була максимальною. Усталеною є практика, коли D= 1/J з (q=180о). У цьому випадку сигнали четвертинних і метиленових атомів вуглецю позитивні, а сигнали метинових і метильних груп – негативні, якщо їх зфазувати так, як це робиться у звичайному вуглецевому спектрі. Прикладом відредагованого таким чином вуглецевого спектру є спектр камфори, 4.1, що зображений на Рис. 4.54б.
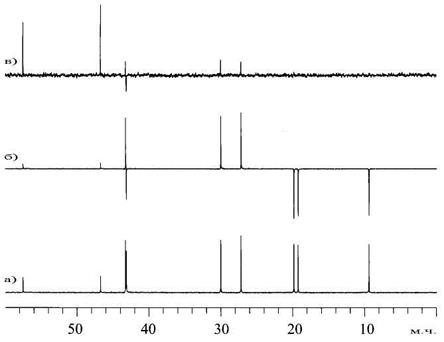
Рис. 4.54. Вуглецевий спектр камфори 4.1 відредагований за допомогою послідовності J-модульованої спін-луни. (a) Звичайний вуглецевий спектр (карбоніл не показаний), і відредаговані спектри з (б) D= 1/J (q=180°) і (в) D= 1/2J (q = 90°) вважалося, що J=130 Гц. Викривлення сигналів протонованих атомів вуглецю в (в) пов'язані з розходженнями в КССВ для різних атомів вуглецю
Часто відредаговані спектри представляють у вигляді, коли сигнали СН позитивні, а сигнали метиленових груп – негативні. Для того, щоб отримати такі спектри достатньо фазу сигналів змінити на 180о за допомогою відповідної фазової корекції. Таким чином, мультиплетність вуглецевих сигналів виявляється закодованою в знаку сигналу. При цьому повертається частина інформації, що губиться при декаплінгу. У спектрах, які записані за допомогою даної послідовності, зберігається підвищення інтенсивності сигналів внаслідок ЯЕО. Якщо вибрати D= 1/2J с., то інтенсивність сигналів всіх протонованих вуглеців, як це витікає з Рис. 4.53, буде дорівнювати нулю і у спектрі залишаться тільки сигнали четвертинних протонів (Рис. 4.54в). Точність редагування істотно залежить від правильності вибору інтервалу D, який визначається величиною J.
Оскільки в реальних молекулах КССВ перебувають у певному діапазоні, доводиться вибирати деяке компромісне значення D. Протон-вуглецеві КССВ через один зв'язок лежать у діапазоні від 125 до 250 Гц, хоча найчастіше зустрічаються їхні величини від 130 до 170 Гц (Табл. 4.2). Тому для молекул, що містять ароматичні фрагменти і електронегативні групи в аліфатичному ланцюгу, типова величина D = 7 мілісекунд (1JCН = 140 Гц). Якщо реальні КССВ перебувають далеко від цього діапазону, то відповідні сигнали можуть мати несподівану фазу і інтенсивність. Так буває при вивченні похідних ацетилену, для яких характерні значно більші КССВ. Тому, для отримання оптимальних результатів цим методом іноді доводиться дещо змінити тривалість інтервалу D. При цьому можна орієнтуватись на типові величини гетероядерних КССВ, що наведені в Табл.. 4.1.
Таблиця 4.1. Типові діапазони для протон-вуглецевих КССВ через один зв'язок
| Оточення атому вуглецю | Типовий діапазон 1JCH (Гц) |
| Аліфатичний, CHn- | 125-135 |
| Аліфатичний, CHn (X = N, O, S) | 135-155 |
| Алкен | 155-170 |
| Алкін | 240-250 |
| Ароматичний | 155-165 |
Експерименти спінової луни легко реалізувати, оскільки вони не вимагають настроювання протонних імпульсів. Хоча історично вони були розроблені першими, зараз вони застосовуються мало, оскільки витіснені більш досконалими методиками. Експеримент може бути виконаним і з вмиканням декаплера тільки на період збору даних. В цьому випадку по каналу протонів подається додатковий 180о імпульс. У даному варіанті імпульсної послідовності інтервал D розбивається на два інтервали по 1/2J (Рис. 4.51б), що розділені 180о імпульсом, який подається одночасно на протони і на атоми вуглецю. У такому варіанті зберігається рефокусування вуглецевих зсувів але під час другого періоду D/2 відбувається еволюція векторів, пов'язаних зі ССВ. Тут, як і в експерименті з переривчастим декаплером, загальний період еволюції дорівнює 1/2J і отримуються ідентичні спектри. Обидва варіанти редагування є практично ідентичними, але імпульсний варіант дещо менш чутливий до недосконалості експерименту. Це найбільш коротка послідовність, що реалізує гетероядерну спінову луну. Вона використовується як фрагмент більш складних імпульсних послідовностей.
Дата добавления: 2015-08-11; просмотров: 1089;
