Спінова луна

Розглянувши, як за допомогою векторної моделі можна представити хімічні зсуви та розщеплення сигналів, зараз ми подивимося, як у простому багатоімпульсному експерименті можна маніпулювати цими векторами. Тут ми надамо простий вступ у використання векторної моделі для розуміння того, що відбувається під час роботи імпульсної послідовності. У багатьох експериментах є проміжки часу, під час яких намагніченості дозволяють просто прецесувати. При цьому відбувається розпад вихідного сумарного вектора намагніченості на ряд векторів, відповідно до хімічних зсувів і спін-спінових розщеплень окремих ядер. Такий процес надалі будемо називати еволюцією спінів. Період еволюції необхідний для того, щоб компоненти намагніченості набули орієнтації, що необхідна для дії наступних імпульсів або збору даних. Для того, щоб це проілюструвати, розглянемо один з основних будівельних елементів імпульсних послідовностей - спінову луну.

Насамперед розглянемо випадок, коли є два нееквівалентних протони А та Х з константою спін-спінової взаємодії (КССВ) J_AX. Нехай на систему впливає проста двохімпульсна послідовність, що зображена на Рис. 1.33.

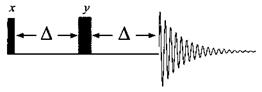
Рис 1.33.Базова послідовність спінової луни

Для простоти ми знову будемо розглядати роздільно ефекти хімічного зсуву та ССВ. Почнемо з хімічного зсуву і припустимо, що опорна частота імпульсу збігається з хімічним зсувом ядра А (Рис. 1.34).

Рис. 2.15.Рефокусування еволюції хімічних зсувів за допомогою послідовності спінової луни.

Рис. 1.34.Рефокусування еволюції хімічних зсувів за допомогою послідовності спінової луни.

Початковий 90^о імпульс індукує поперечну намагніченість ядер А та Х, причому по закінченні імпульсу обидва вектори спрямовані вздовж осі у. Після цього вектор Х прецесує протягом інтервалу часу D (вектор А в системі координат, що обертається залишається нерухомим). Другий імпульс 180^о_у (відзначте, що він спрямований уздовж осі у) обертає намагніченість Х на 180^о навколо осі у і тому знову розміщує її в площині х-у, однак, тепер уже позаду вектора А. Оскільки намагніченість А нерухома і розташована уздовж осі у, другий імпульс на неї не діє. Під час другого періоду часу D, намагніченість Х повернеться на той самий кут, що і під час першого періоду часу і наприкінці послідовності досягне вихідної точки - вектора А. Таким чином, через період 2D між векторами А та Х не буде ніякого фазового зсуву, незважаючи на розходження в їхніх хімічних зсувах. Тобто розходження в хімічних зсувах ядер А і Х зникають. Говорять, що спінова луна рефокусує хімічні зсуви. Перший і другий періоди часу D називають відповідно періодами розфазування та рефокусування (рефазування).

Розглянемо тепер ефект наявності між спінами А та Х спін-спінової взаємодії. Опорна частота імпульсу при цьому, як і раніше, збігається з хімічним зсувом ядра А. Ефекти хімічних зсувів будемо ігнорувати, оскільки ми вже знаємо, що наприкінці імпульсної послідовності вони рефокусуються. Як і раніше, після першого імпульсу вектори, що описують компоненти дублетів, рухаються в протилежних напрямках. Після другого 180^о_у імпульсу рух векторів відбувається в зворотному напрямку. По закінченні послідовності ці компоненти здобувають початкову орієнтацію. З цього погляду два компоненти дублетів у результаті дії послідовності рефокусуються, точно так само, як і описані вище хімічні зсуви. Однак слід враховувати, що послідовність впливає також і на партнера по ССВ, ядро Х. При цьому треба згадати, за рахунок чого утворюються компоненти дублетів. Вони виникають внаслідок того, що спін А взаємодіє зі спіном Х, який може мати дві орієнтації, a і b. Якщо спін Х має одну орієнтацію, то утвориться сильнопольний компонент дублету спіна А. Якщо ж спін Х має іншу орієнтацію, утворюється слабопольний компонент дублету спіна А. оскільки населеності станів a і b приблизно однакові, то половинки дублетів мають однакову інтенсивність (незначна різниця в населеностях станів практично не впливає на інтенсивності компонентів). Ефект впливу 180^о імпульсу на спіни Х полягає в інвертуванні спінових станів. Тому спіни А, які раніше були пов'язані з X_a тепер виявилися пов'язаними з X_b і навпаки. Це означає, що вектор, який рухався швидше, тепер починає рухатися повільніше й навпаки. Кінцевий результат представлений на Рис. 1.35а.

Рис. 1.35.Вплив спінової луни на скалярні розщеплення. Показано для двох зв'язаних спінів A і X. (a) Гомоядерна спін-луна. У цьому випадку 180° імпульс впливає на обидва спіни. При дії послідовності має місце еволюція розщеплень. (б) Гетероядерна спина-луна. У цьому випадку 180° імпульс впливає тільки на один спін. Внаслідок цього відбувається рефокусування гетероядерних розщеплень. Якщо одночасно подати 180^о імпульси на частотах обох спінів, то еволюція розщеплень буде відбуватися так само, як і в (а) .

Дві половинки дублетів після другого імпульсу продовжують розфазування, тому наприкінці періоду 2D ССВ (J-взаємодія), на відміну від хімічних зсувів, продовжує еволюцію. Таким чином, гомоядерна ССВ не рефокусується в результаті дії послідовності спінової луни. Термін «гомоядерна» у попередньому реченні підкреслює те, що для випадку, коли взаємодіють ядра різних типів, наприклад ¹Н и ¹³С, ситуація може виявитися трохи іншою. У цьому випадку 180^о імпульс впливає тільки на одне з магнітних ядер, тоді як інше ядро цього імпульсу не відчуває. При цьому відбувається рефокусування гетероядерної ССВ (Рис. 1.32б).

Якщо ж одночасно прикласти імпульси по двох каналах опромінення на частотах обох ядер, що зв’язані ССВ, одержимо ситуацію, аналогічну до гомоядерної взаємодії.

Використання в описаній вище послідовності замість 180^о_х імпульсу 180^о_у імпульсу дозволяє одержати більш наочну картину. Ефекти рефокусування хімічних зсувів і ССВ, що описані вище, відбуваються і при впливі 180^о_у імпульсу з тією відмінністю, що в цьому випадку рефокусовані вектори спрямовані уздовж осі -у, а не +у. Ще однією корисною особливістю послідовності спінової луни є знищення ефектів, пов'язаних з неоднорідністю статичного магнітного поля, оскільки вони можуть бути представлені як внесок ядер зразка з неоднаковими хімічними зсувами. Важливість послідовності спінової луни в сучасних методиках ЯМР важко переоцінити. Вона дозволяє проводити експерименти, що базуються на розбіжності фаз сигналів, не піклуючись про наявні розходження в хімічних зсувах. Це дає нам змогу маніпулювати векторами компонентів мультиплетів, утворених завдяки ССВ із сусідніми атомами, що дозволяє реалізувати багато методик сучасного ЯМР.