Линейные дифференциальные уравнения первого порядка. Физические задачи, приводящие к решению дифференциальных уравнений первого порядка

Уравнения вида

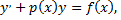
где и – непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

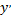Название уравнения объясняется тем, что неизвестная функция и ее производная входят в уравнение линейно, т.е. в первой степени. Если то уравнение называется линейным однородным. Если 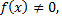то уравнение называется линейным неоднородным.

Для нахождения общего решения дифференциального уравнения

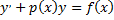
можно воспользоваться двумя методами.

Первый метод – это метод вариации постоянной. В этом методе сначала находят общее решение линейного однородного уравнения

соответствующего данному неоднородному уравнению. Вышеуказанное уравнение является уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, получим

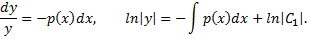
Находим общее решение уравнения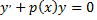

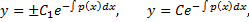
где 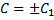– произвольная постоянная.

Теперь найдем общее решение дифференциального уравнения

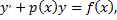
где 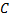будем считать не постоянной, а новой неизвестной функцией от т.е. в виде

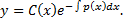
Чтобы найти 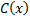подставим функцию 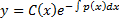в уравнение

.

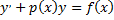Получим

Интегрируя, находим

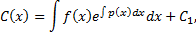
где 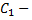произвольная постоянная. Подставляя найденное выражение для 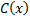в

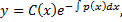
получим общее решение линейного дифференциального уравнения

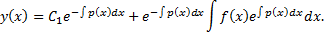
Линейные дифференциальные уравнения можно решить методом Бернулли, суть которого заключается в следующем. Введем две неизвестные функци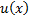и и 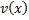по формуле

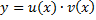
- это подстановка Бернулли. Тогда

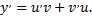
Подставив выражения для и 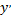в уравнение

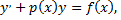
получим уравнение

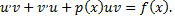
Пользуясь тем, что одна из неизвестных функций, например может быть выбрана произвольно. Поскольку только произведение 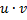должно удовлетворять уравнению

,

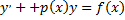выбираем в качестве 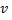любое частное решение уравнения

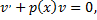
обращающее в нуль коэффициент перед 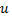в уравнении

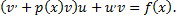
После этого данное уравнение превращается в уравнение

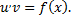
Найдя общее решение 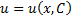последнего уравнения, придем к общему решению уравнения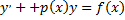

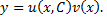
Таким образом, интегрирование уравнения

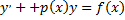
сводится к интегрированию двух уравнений с разделяющимися переменными.

Рассмотрим пример. Проинтегрировать уравнение

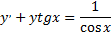
методом Бернулли и решить задачу Коши при начальном условии

Сделав подстановку 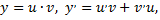получим

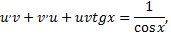
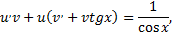
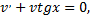
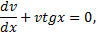
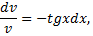
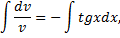
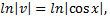
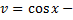частное решение.

Далее ищем общее решение уравнения

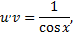
где

Получим

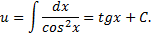
Тогда общее решение исходного уравнения

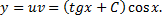
Из него выделяем частное решение, удовлетворяющее начальному условию

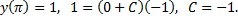
Подставляя значение 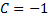в общее решение, получаем частное решение исходного уравнения

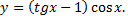
Дифференциальное уравнение

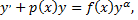
где 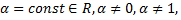а также любое уравнение, с помощью алгебраических преобразований приводящие к уравнению

,

называется уравнением Бернулли.

Путем введения новой функции 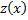по формуле 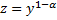уравнение Бернулли сводится к линейному уравнению относительно этой функции

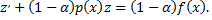
Решив данное уравнение одним из описанных выше методов, найдем а затем и

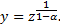
К дифференциальным уравнениям первого порядка приводят различные физические задачи. Основную трудность при их решении представляет составление дифференциальных уравнений. Универсального метода составления не существует, каждая задача требует индивидуального подхода, основанного на понимании законов физики, и умения переводить физические задачи на математический язык.

Рассмотрим пример. Закон естественного роста – это закон, согласно которому скорость роста вещества прямо пропорциональна его количеству. Найдем формулу для определения изменения количества вещества в зависимости от времени 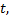считая, что в начальный момент 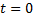количество вещества было равно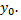

Здесь независимой переменной является время 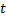, а искомой величиной – количество вещества в любой момент времени. Скорость роста вещества есть скорость изменения величины в зависимости от переменной 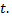Используя физический смысл производной, можно записать закон естественного роста следующим образом

где коэффициент пропорциональности. Данное уравнение описывает многие процессы размножения. Решение этого уравнения, удовлетворяющее начальным условиям

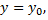имеет вид

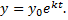
Эта формула выражает закон естественного роста, согласно которому, например, происходит размножение бактерий, рост кристаллов и т.д.