Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Общее решение линейного неоднородного уравнения
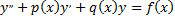
имеет вид 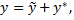 где
где 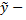 общее решение соответствующего ему однородного уравнения
общее решение соответствующего ему однородного уравнения
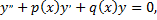
а 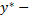 одно из частных решений уравнения
одно из частных решений уравнения
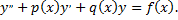
Для того, чтобы решить линейное неоднородное уравнение с постоянными коэффициентами, необходимо:
1) найти его фундаментальную систему решений;
2) составить общее решение 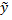 однородного уравнения;
однородного уравнения;
3) найти частное решение 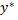 уравнения
уравнения

4) по формуле 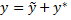 получить общее решение .
получить общее решение .
Если известна фундаментальная система решений уравнения
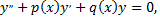
то частное решение 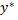 уравнения
уравнения
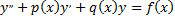
можно найти методом вариации произвольных постоянных, согласно которому 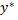 всегда представимо в виде
всегда представимо в виде

где 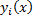 образуют фундаментальную систему уравнения
образуют фундаментальную систему уравнения
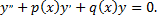
Особенности интегрирования неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами со специальной правой частью. Метод вариации произвольной постоянной
В различных инженерных приложениях правая часть уравнения
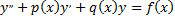
во многих случаях имеет специальный вид
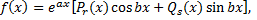
где 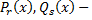 многочлены степени
многочлены степени 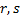 соответственно,
соответственно, 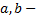 некоторые постоянные числа. Доказано, что во всех случаях, а также и в общем случае, частное решение
некоторые постоянные числа. Доказано, что во всех случаях, а также и в общем случае, частное решение 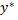 уравнения
уравнения 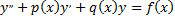 имеет следующую структуру
имеет следующую структуру
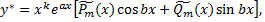
где 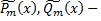 многочлены степени
многочлены степени 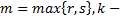 число, равное числу корней характеристического уравнения
число, равное числу корней характеристического уравнения 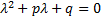 , совпадающему с числом
, совпадающему с числом 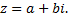 Таким образом,
Таким образом, 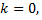 если среди корней
если среди корней 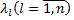 нет числа
нет числа 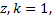 если существует один корень, совпадающий, с
если существует один корень, совпадающий, с 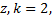 если существует двукратный корень, совпадающий с
если существует двукратный корень, совпадающий с 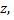 и т.д. Следовательно, согласно формуле
и т.д. Следовательно, согласно формуле
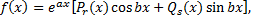
сразу можно определить структуру частного решения  в котором неизвестными являются только коэффициенты многочленов
в котором неизвестными являются только коэффициенты многочленов 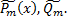 Подставляя решение
Подставляя решение 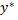 и его производные в уравнение
и его производные в уравнение
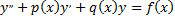
и приравнивая коэффициенты подобных членов слева и справа, получаем необходимое количество линейных алгебраических уравнений для вычисления этих неизвестных коэффициентов. Такой способ нахождения коэффициентов и, тем самым, 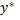 называется методом неопределенных коэффициентов. Следовательно, зная структуру
называется методом неопределенных коэффициентов. Следовательно, зная структуру 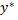 можно найти частное решение с помощью элементарных операций, таких как дифференцирование и решение систем линейных алгебраических уравнений, не применяя операцию интегрирования.
можно найти частное решение с помощью элементарных операций, таких как дифференцирование и решение систем линейных алгебраических уравнений, не применяя операцию интегрирования.
Рассмотрим пример. Найти общее решение уравнения
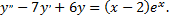
Решим соответствующее однородное уравнения
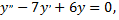
составим соответствующее ему характеристическое уравнение
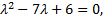
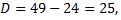
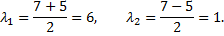
Общее решение соответствующего однородного уравнения

Правая часть исходного дифференциального уравнения специальная, определим ее общий вид
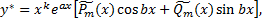
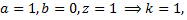


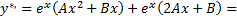
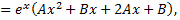


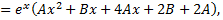
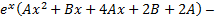
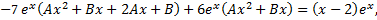
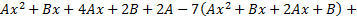
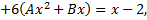
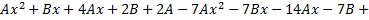
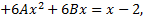
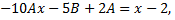

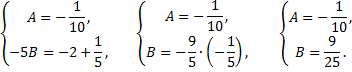
Определив  и
и 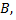 можно записать
можно записать
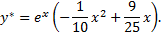
Общим решением исходного дифференциального уравнения является функция
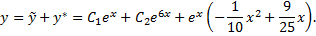
Рассмотрим пример. Найти общее решение уравнения
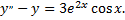
Соответствующее однородное уравнение
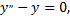
которому соответствует характеристическое уравнение
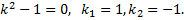
Общее решение однородного уравнения
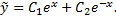
В правой части уравнения – произведение многочлена нулевой степени, показательной и тригонометрической функций 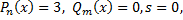 и частное решение ищем в виде
и частное решение ищем в виде

Дифференцируя и подставляя в уравнение, получаем

Приравнивая коэффициенты при 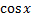 и
и 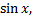 находим
находим
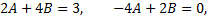
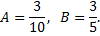
Таким образом, частное решение
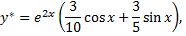
а общее решение уравнения
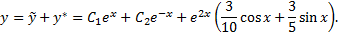
Рассмотрим пример. Найти общее решение уравнения
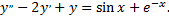
Характеристическое уравнение соответствующего однородного
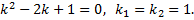
Следовательно, общее решение соответствующего однородного уравнения
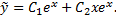
Так как правая часть уравнения состоит из суммы двух функций 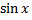 и
и 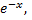 то частное решение данного уравнения можно искать в виде
то частное решение данного уравнения можно искать в виде 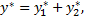 где
где 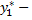 частное решение уравнения
частное решение уравнения 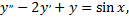 а
а 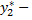 частное решение уравнения
частное решение уравнения 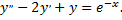
Сначала найдем частное решение 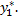 Так как число
Так как число 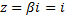 не является корнем характеристического уравнения, то частное решение
не является корнем характеристического уравнения, то частное решение 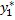 будем искать в виде
будем искать в виде
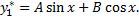
Подставляя 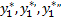 в уравнение
в уравнение 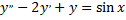 и сравнивая коэффициенты при
и сравнивая коэффициенты при 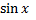 и
и 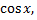 получаем
получаем
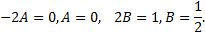
Следовательно
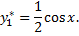
Теперь найдем частное решение 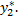 Будем его искать в виде
Будем его искать в виде 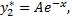 так как
так как 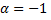 не является корнем характеристического уравнения. Подставляя
не является корнем характеристического уравнения. Подставляя  в уравнение
в уравнение

получим, что 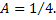 Следовательно,
Следовательно, 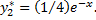
Таким образом, частное решение данного уравнения имеет вид
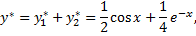
а общее решение

Контрольные вопросы
1. Записать алгоритм решения линейного неоднородного уравнения с постоянными коэффициентами.
2. В каком виде находят решение линейного неоднородного уравнения с постоянными коэффициентами со специальной правой частью?
3. Записать общее решение линейного неоднородного уравнения с постоянными коэффициентами со специальной правой частью?
Дата добавления: 2015-08-11; просмотров: 1510;
