Решение системы линейных дифференциальных уравнений с постоянными коэффициентами
Все сказанное выше верно и для частного случая нормальной системы дифференциальных уравнений, которая имеет вид
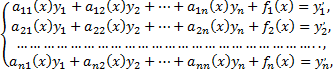
где функции 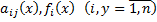 предполагаются непрерывными в некотором интервале
предполагаются непрерывными в некотором интервале 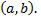 Если все
Если все 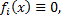 то рассматриваемая система называется однородной, в противном случае неоднородной. Если
то рассматриваемая система называется однородной, в противном случае неоднородной. Если 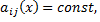 то рассматриваемая система называется линейной с постоянными коэффициентами. Существуют методы, позволяющие проинтегрировать такую систему. Рассмотрим два из них.
то рассматриваемая система называется линейной с постоянными коэффициентами. Существуют методы, позволяющие проинтегрировать такую систему. Рассмотрим два из них.
Первый метод. Составляем характеристическое уравнение
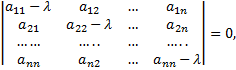
где 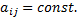 Раскрывая определитель, приходим к алгебраическому уравнению степени
Раскрывая определитель, приходим к алгебраическому уравнению степени  относительно
относительно 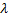 с действительными постоянными коэффициентами, которое имеет
с действительными постоянными коэффициентами, которое имеет  корней.
корней.
Если корни характеристического уравнения действительные и различные 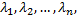 то каждому корню соответствует частное решение вида
то каждому корню соответствует частное решение вида
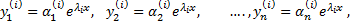
где коэффициенты 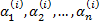 определяются из системы линейных алгебраических уравнений
определяются из системы линейных алгебраических уравнений
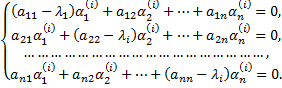
Все частные решения вида
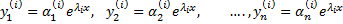
образуют фундаментальную систему решений.
Общее решение однородной системы с постоянными коэффициентами, получаемой из системы

при 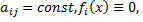 представляет собой следующую совокупность функций, являющихся линейной комбинацией решений
представляет собой следующую совокупность функций, являющихся линейной комбинацией решений
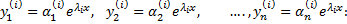
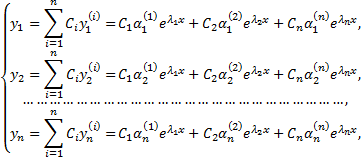
где 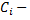 произвольные постоянные.
произвольные постоянные.
Рассмотрим пример. Найти общее решение однородной системы
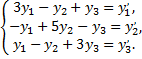
Характеристическое уравнение данной системы
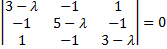
имеет различные действительные корни 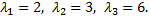 Для каждого из них составляем систему
Для каждого из них составляем систему
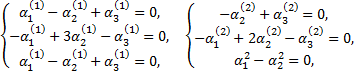
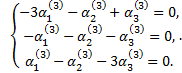
Так как определители этих систем равны нулю, то каждая из них имеет бесчисленное множество решений. В данном случае можно выбрать те решения, для которых 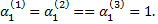 Тогда получим следующие решения систем: если
Тогда получим следующие решения систем: если  то
то
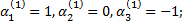
если 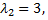 то
то
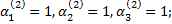
если  то
то
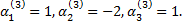
Это приводит к фундаментальной системе решений
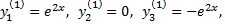
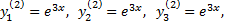
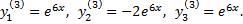
Линейная комбинация этих решений с учетом совокупности функций
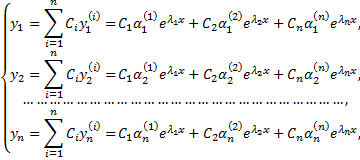
дает общее решение исходной системы
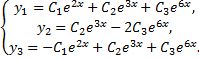
Второй случай. Корни 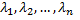 характеристического уравнения
характеристического уравнения
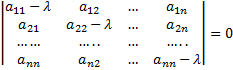
различные, но среди них имеются комплексные. Известно, что в этом случае каждой паре комплексно – сопряженных корней  характеристического уравнения соответствует пара частных решений
характеристического уравнения соответствует пара частных решений
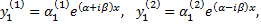
где 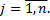 Коэффициенты
Коэффициенты 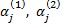 определяются из системы
определяются из системы
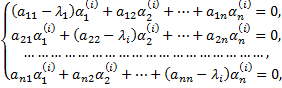
соответственно для 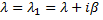 и
и  Коэффициенты
Коэффициенты 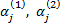 оказываются, как правило, комплексными числами, а соответствующие им функции
оказываются, как правило, комплексными числами, а соответствующие им функции 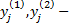 комплексными функциями. Выделяя мнимую и действительную части функций
комплексными функциями. Выделяя мнимую и действительную части функций 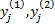 и пользуясь тем, что для линейных уравнений с действительными коэффициентами и мнимая, и действительная части решения также являются решениями, получаем пару частных действительных решений однородной системы.
и пользуясь тем, что для линейных уравнений с действительными коэффициентами и мнимая, и действительная части решения также являются решениями, получаем пару частных действительных решений однородной системы.
Рассмотрим пример. Найти общее решение системы
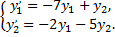
Характеристическое уравнение системы
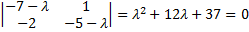
имеет корни 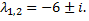 Получаем
Получаем
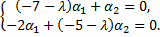
Корню 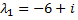 соответствует система для вычисления
соответствует система для вычисления 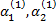
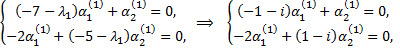
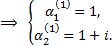
Согласно формуле 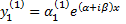 получаем частное решение
получаем частное решение
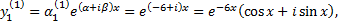
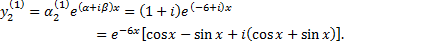
Взяв в отдельности действительные и мнимые части в решении, получим два решения в действительной форме, образующих фундаментальную систему решений системы
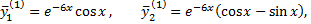
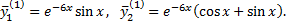
Тогда общее решение системы имеет вид
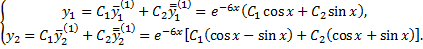
Третий случай. Среди корней 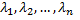 характеристического уравнения имеются кратные. В этом случае поступаем следующим образом. Пусть
характеристического уравнения имеются кратные. В этом случае поступаем следующим образом. Пусть 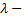 корень кратности
корень кратности 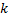 характеристического уравнения. Тогда решение системы, для которой
характеристического уравнения. Тогда решение системы, для которой 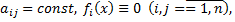 соответствующее этому
соответствующее этому  кратному корню, ищем в виде
кратному корню, ищем в виде
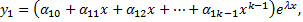
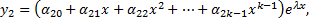
……………………………………………………………………………

Числа 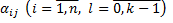 находим, подставляя функции
находим, подставляя функции 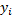 и их производные
и их производные  в исходную систему при указанных ограничениях на
в исходную систему при указанных ограничениях на 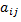 и
и 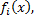 а затем приравниваем коэффициенты при одинаковых степенях
а затем приравниваем коэффициенты при одинаковых степенях  в левых и правых частях полученных равенств. В результате проведенных действий из всех чисел
в левых и правых частях полученных равенств. В результате проведенных действий из всех чисел  всегда остаются в качестве свободных параметров, которые принимаются за произвольные постоянные.
всегда остаются в качестве свободных параметров, которые принимаются за произвольные постоянные.
Рассмотрим пример. Найти общее решение системы

Характеристическое уравнение системы
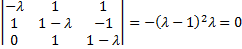
имеет двукратный 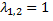 и однократный
и однократный 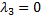 корни. Двукратному корню
корни. Двукратному корню 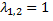 соответствует решение вида
соответствует решение вида
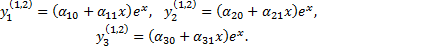
Коэффициенты 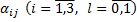 определяются из системы, полученной подстановкой выражений для
определяются из системы, полученной подстановкой выражений для 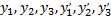 в исходную систему. После сокращения на
в исходную систему. После сокращения на 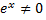 имеем
имеем
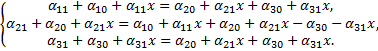
Приравнивая коэффициенты при одинаковых степенях 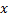 слева и справа, получаем систему
слева и справа, получаем систему
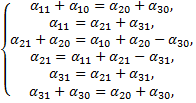
из которой находим, что
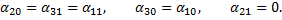
Числа 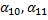 можно считать произвольными параметрами. Обозначим их через
можно считать произвольными параметрами. Обозначим их через  и
и 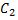 соответственно. Тогда решение запишется в виде
соответственно. Тогда решение запишется в виде
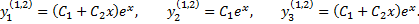
Корню 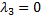 соответствует решение
соответствует решение

где числа  определяется из системы
определяется из системы
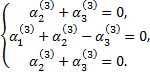
Ее решение 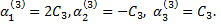 Следовательно, соответствующее корню
Следовательно, соответствующее корню
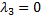 решение исходной системы имеет вид
решение исходной системы имеет вид

где 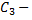 произвольная постоянная.
произвольная постоянная.
Общее решение исходной систему записывается в виде
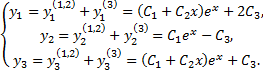
Если система неоднородная, то, зная общее решение вида

соответствующей однородной системы, можно найти общее решение исходной неоднородной системы методом вариации произвольных постоянных 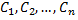 в решении
в решении
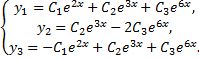
Общее решение неоднородной системы всегда можно записать в данном виде, заменив произвольные постоянные 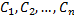 соответственно функциями
соответственно функциями 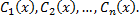 Эти функции определяются с помощью данной неоднородной системы. В систему подставляют
Эти функции определяются с помощью данной неоднородной системы. В систему подставляют  получают линейную систему
получают линейную систему  алгебраических уравнений относительно
алгебраических уравнений относительно 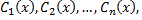 решение которой всегда существует и представимо в виде
решение которой всегда существует и представимо в виде
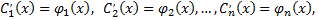
где 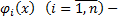 известные функции. Интегрируя эти равенства, находим
известные функции. Интегрируя эти равенства, находим
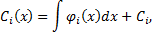
где 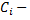 произвольные постоянные.
произвольные постоянные.
Рассмотрим пример. Решить задачу Коши
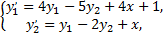
заданы начальные условия 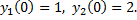
Найдем общее решение соответствующей однородной системы
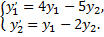
Корни ее характеристического уравнения  общее решение ищем в виде
общее решение ищем в виде
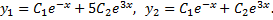
Пусть в данном решении  и
и 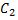 являются неизвестными функциями
являются неизвестными функциями 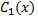 и
и 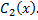 Потребуем, чтобы
Потребуем, чтобы 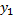 и
и 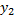 были решением исходной системы. Находим
были решением исходной системы. Находим
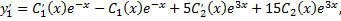
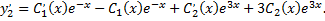
Подставляем выражения для  в исходную систему, приводим подобные члены и получаем систему
в исходную систему, приводим подобные члены и получаем систему
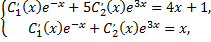
откуда
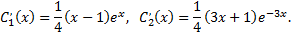
Проинтегрируем последние равенства
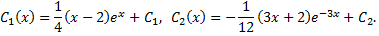
Подставляя 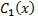 и
и 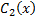 в равенства
в равенства 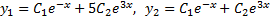 вместо
вместо  и
и 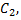 получаем общее решение исходной неоднородной системы
получаем общее решение исходной неоднородной системы
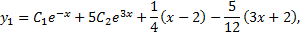
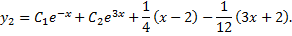
Используя начальные условия, получим систему для определения постоянных  и
и  :
:

откуда 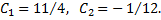
Решением задачи Коши будет следующее частное решение
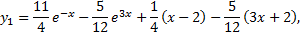
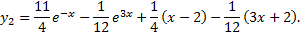
Контрольные вопросы
1. Что называют порядком нормальной системы?
2. Дать определение решению нормальной системы в заданном интервале?
3. Дать формулировку Задачи Коши для системы дифференциальных уравнений первого порядка.
4. Что называют общим решением нормальной системы?
5. Дать определение частного решения нормальной системы дифференциальных уравнений первого порядка.
Дата добавления: 2015-08-11; просмотров: 7004;
