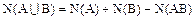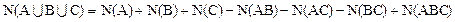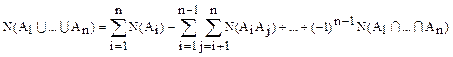Конечные множества и их элементы.
N(A) – количество элементов множества А
Доказать самостоятельно.
Понятие алгебры множеств σ – алгебры.
Множество А подмножеств множества U называется алгеброй множеств, если:
- Ø
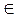 А ; U
А ; U 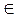 А;
А; -
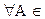 А;
А; 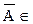 А
А -
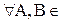 А
А
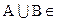 А
А
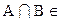 А
А
Алгебра множеств называется σ – алгеброй, если из условия, что А1; A2; A3; ... 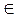 А следует, что
А следует, что 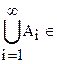 А;
А; 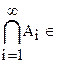 А
А
Пусть γ– некоторая система множеств, тогда наименьшая алгебра, содержащая γ называется алгеброй, порожденной системой γ.
Наименьшая σ – алгебра содержит систему множеств γ называется σ – алгеброй порожденной системой γ
Теорема: 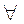 конечное разбиение множества U порождает алгебру множеств.
конечное разбиение множества U порождает алгебру множеств.
Обратное 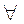 алгебра множеств порождается некоторым конечным разбиением.
алгебра множеств порождается некоторым конечным разбиением.
Борелевские множества. Борелевская σ – алгебра.
σ – алгебра ß числовых множеств, порожденная всевозможными интервалами и полуинтервалами вида 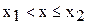 называется борелевским.
называется борелевским.
Множества составляющие ß называется борелевскими.
Дата добавления: 2015-07-30; просмотров: 1295;