Выбор с возвращением.
| Выборка с возвращением, упорядоченная. | Выборка с возвращением, неупорядоченная. |
 Имеется хранилище с n различными предметами.
Имеется хранилище с n различными предметами.
 Имеется k занумерованных ящиков.
Из хранилища берем один случайный предмет. Информацию о нем фиксируем в первой ячейке. Сам предмет возвращаем в хранилище. Затем берем следующий предмет и информацию фиксируем во второй ячейке. И т.д.
Имеется k занумерованных ящиков.
Из хранилища берем один случайный предмет. Информацию о нем фиксируем в первой ячейке. Сам предмет возвращаем в хранилище. Затем берем следующий предмет и информацию фиксируем во второй ячейке. И т.д.
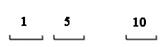
  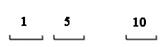
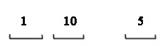 В данной схеме различными считаются варианты, которые отличаются хотя бы одной позицией.
Общее число
В данной схеме различными считаются варианты, которые отличаются хотя бы одной позицией.
Общее число 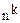 ; ; 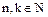
|
 Имеется хранилище с n различными предметами.
Имеется хранилище с n различными предметами.
 Имеется ящик объемом k.
Из хранилища берем один случайный предмет. Информацию о нем фиксируем в ящике. Сам предмет возвращаем в хранилище. Затем берем следующий предмет и информацию фиксируем в ящике. И т.д.
Имеется ящик объемом k.
Из хранилища берем один случайный предмет. Информацию о нем фиксируем в ящике. Сам предмет возвращаем в хранилище. Затем берем следующий предмет и информацию фиксируем в ящике. И т.д.
 В данной схеме различными считаются варианты, которые отличаются набором элементов.
В данной схеме различными считаются варианты, которые отличаются набором элементов.
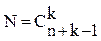 .
Доказательство.
Используем математическую индукцию. .
Доказательство.
Используем математическую индукцию.
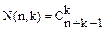 1. База индукции.
K=1;
1. База индукции.
K=1; 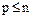 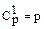 2. Предположим, что для некоторого k N(p , k ) =
2. Предположим, что для некоторого k N(p , k ) = 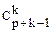  Докажем, что для k+1 формула справедлива
Докажем, что для k+1 формула справедлива 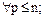 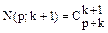 .
а – наименьший номер элемента попавшего во второе хранилище. Если а = 1, то оставшиеся k позиций могут быть заполнены .
а – наименьший номер элемента попавшего во второе хранилище. Если а = 1, то оставшиеся k позиций могут быть заполнены  .
a=1 → .
a=1 → 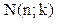 a=2 →
a=2 → 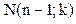 a=3 →
a=3 → 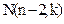 …..
a=n-1 →
…..
a=n-1 → 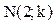 a=n →
a=n → 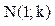

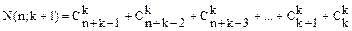
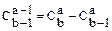

|
Дата добавления: 2015-07-30; просмотров: 1292;
