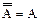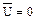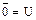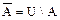Операции над множествами.
- Объединение – объединение множеств А и В называется множество С, которое состоит из всех элементов входящих в хотя бы в одно из этих множеств.
A 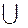 B = {c: (c
B = {c: (c 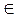 A)
A) 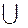 (c
(c 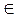 B)}
B)}

1. A 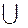 B = B
B = B 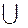 A – коммутативность
A – коммутативность
2. A 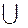 (B
(B 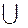 C) = (A
C) = (A 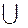 B)
B) 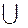 C = A
C = A 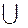 B
B 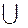 C – ассоциативность
C – ассоциативность
3. A 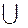 A = A – идемпотентность
A = A – идемпотентность
4. A 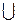 ø = A
ø = A
5. (B 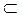 A) → B
A) → B 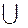 A = A
A = A
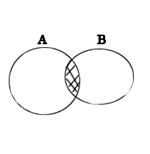
- Пересечение множеств А и В называется множество С, которое состоит из всех элементов одновременно входящих в оба множества.
A 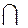 B={c: (c
B={c: (c 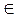 A)&(c
A)&(c 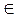 B)}
B)}
1. A 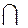 B = B
B = B 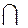 A – коммутативность
A – коммутативность
2. A 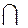 (B
(B 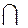 C) = (A
C) = (A 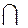 B)
B) 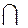 C = A
C = A 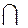 B
B 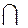 C – ассоциативность
C – ассоциативность
3. A 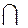 A = A – идемпотентность
A = A – идемпотентность
4. A 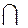 ø = ø
ø = ø
5. (B 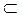 A) → B
A) → B 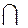 A = B
A = B
Если А 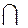 В = Ø, то такие множества называются не пересекающимися
В = Ø, то такие множества называются не пересекающимися
Система множеств А1; A2; A3; ... An называется разбиением множества А, если выполняется два условия:
- А1
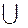 A2
A2 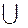 A3
A3 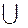 ...
... 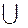 An = A
An = A - Ai
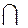 Aj =
Aj = 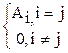
- Разностью множеств А и В, называется множество С, которое состоит из всех элементов множества А не входящих в В.
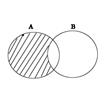
А \ В = {c: (c 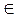 A)&(c
A)&(c 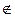 B)}
B)}
А \ В = A \ (A 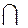 B)
B)
- Симметрической разностью множеств А и В, называется множество С, которое состоит из всех элементов входящих либо только в А, либо только в В.
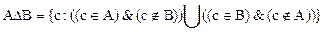
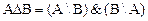

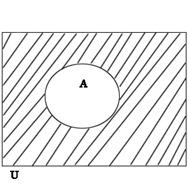
- Понятие универсального множества. Операция дополнение.
Множество U, называется универсальным для множеств А1; A2; A3; ... An , если все эти множества входят в множество U как подмножества.
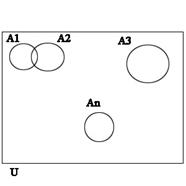
Множество 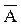 , называется дополнительным множеством или дополнением множества, если оно состоит из всех элементов универсального множества не принадлежащих множеству А.
, называется дополнительным множеством или дополнением множества, если оно состоит из всех элементов универсального множества не принадлежащих множеству А.
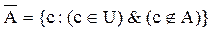
Дата добавления: 2015-07-30; просмотров: 1147;