Ряд Тейлора Определение

Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд 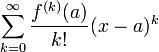называется рядом Тейлора функции f в точке a.

В случае, если a = 0, этот ряд также называется рядом Макло́рена.

Свойства

• Если f есть аналитическая функция, то её ряд Тейлора в любой точке a области определения f сходится к f в некоторой окрестности a.
• Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности a. Например, Коши предложил такой пример:

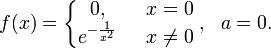
(ХЗ нужна ли?)Теорема

Пусть функция f(x) имеет n + 1 производную в некоторой окрестности точки a, U(a,ε)

Пусть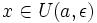

Пусть p — произвольное положительное число,

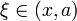тогда: точка при x < a или 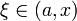при x > a:

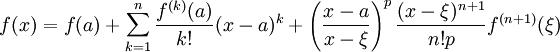
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).

Классическое определение вероятности. Статистическое понятие вероятности. Геометрический подход к вероятности. Аксиоматическое построение теории вероятностей. Свойства вероятностей.