Интегральное представление гармонических функций
Пусть 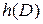 – множество всех гармонических в
– множество всех гармонических в 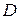 функций;
функций; 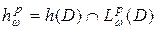 , то есть
, то есть
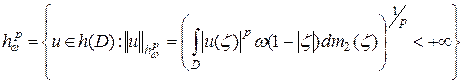 .
.
В этом параграфе мы построим аналог представления (2.6) для функций из класса 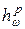 . Сначала заметим, что из (2.6) непосредственно следует представление
. Сначала заметим, что из (2.6) непосредственно следует представление
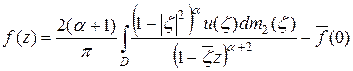 .
.
Действительно, если 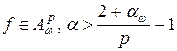 , то по формуле (2.6)
, то по формуле (2.6)
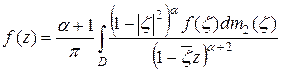 . (7)
. (7)
Но нетрудно увидеть, что
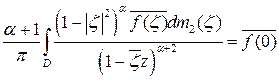 . (8)
. (8)
Поэтому, суммируя равенства (7) и (8), окончательно получим:
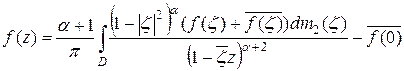 .
.
Следовательно,
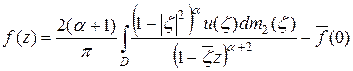 . (9)
. (9)
Формула (9) является аналогом формулы Шварца для классов Харди Из (9) непосредственно вытекает:
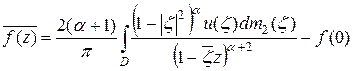 . (10)
. (10)
Суммируя формулы (9) и (10), получим:
 (11)
(11)
Положим
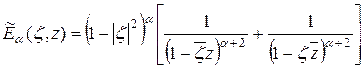 ,
, 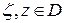 ;
;
тогда из (11) имеем:
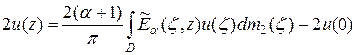
или
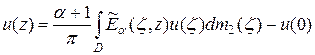 .
.
Но учитывая, что 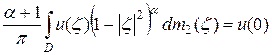 , окончательно получаем следующее утверждение:
, окончательно получаем следующее утверждение:
Теорема 6. Пусть 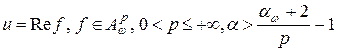 . Тогда справедливы следующие представления
. Тогда справедливы следующие представления
а) 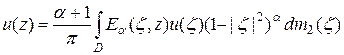 ,
,
где  .
.
б) 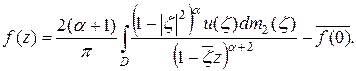
4. Ограниченные проекторы в пространствах 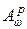 и
и 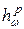 при
при 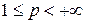
Рассмотрим интегральный оператор в 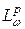 с ядром
с ядром
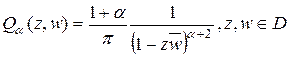 :
:
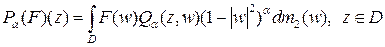 .
.
Очевидно, что 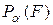 – аналитическая функция в
– аналитическая функция в 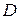 для произвольной функции
для произвольной функции  , при условии, что
, при условии, что 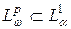 , где
, где
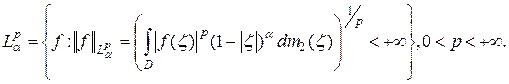
В этом параграфе мы дадим полную характеризацию тех 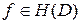 , для которых справедливо представление (2.7) при некотором
, для которых справедливо представление (2.7) при некотором  . С этой целью сначала докажем следующее элементарное утверждение.
. С этой целью сначала докажем следующее элементарное утверждение.
Пусть, как и прежде, 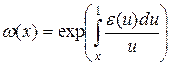 , где
, где 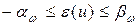 , при этом
, при этом 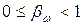 , также
, также 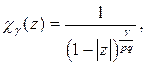
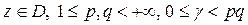 .
.
Лемма 1. Пусть 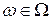 , при этом
, при этом 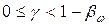 , тогда справедливы оценки:
, тогда справедливы оценки:
а) 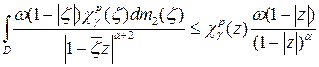 при всех
при всех 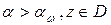 .
.
б) 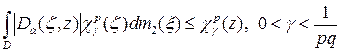 .
.
Напомним, что  .
.
Доказательство. Положим
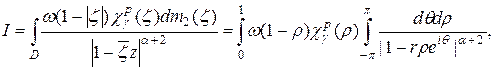 ,
,
где 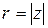 . Учитывая тождество
. Учитывая тождество
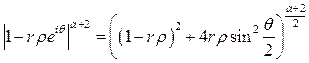
и равенство
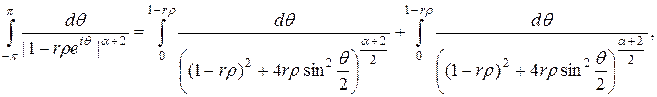
легко установить оценку
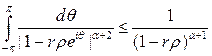 при
при  .
.
Поэтому
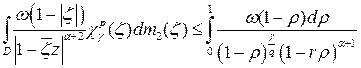 .
.
Положим
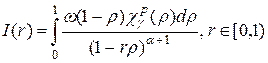 .
.
Очевидно,
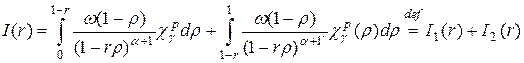 .
.
Нетрудно заметить, что
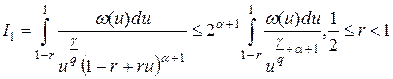 .
.
Интегрируя по частям в последнем интеграле, получаем:
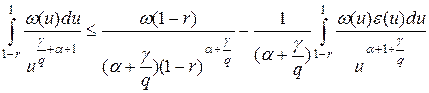 .
.
Отсюда, учитывая что 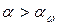 , выводим:
, выводим:
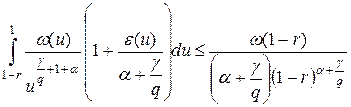
или
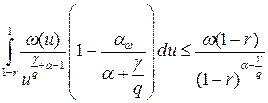 ,
,
то есть
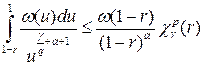 . (2.12)
. (2.12)
Перейдём к оценке 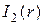 . Проводя аналогичные рассуждения, получаем:
. Проводя аналогичные рассуждения, получаем:
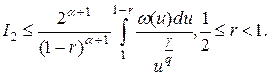
Интегрируя в последнем интеграле по частям, приходим к равенству
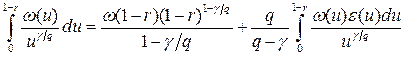 ,
,
то есть
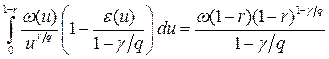 .
.
Отсюда, учитывая, что 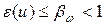 , окончательно получаем:
, окончательно получаем:
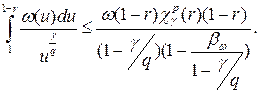 (13)
(13)
Объединяя оценки (12) и (13), приходим к первому утверждению леммы. Теперь докажем неравенство б). В силу леммы 1 имеем:
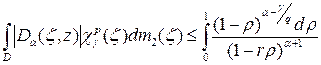 .
.
Повторяя рассуждения части а) доказательства, приходим к оценке
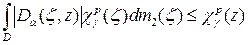 . □
. □
Следующее утверждение известно как тест Шура
Теорема 7. Пусть  –
–  -измеримое множество с неотрицательной мерой
-измеримое множество с неотрицательной мерой  на
на  ,
, 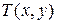 – неотрицательная функция на
– неотрицательная функция на 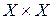 , оператор
, оператор  определён на множестве
определён на множестве  -измеримых функций
-измеримых функций 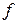 следующим образом
следующим образом
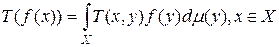 ,
,
причём функция 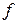 такая, что интеграл сходится к
такая, что интеграл сходится к  почти всюду.
почти всюду.
Тогда если 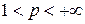 и существуют строго положительная
и существуют строго положительная 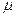 -измеримая функция
-измеримая функция 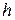 на
на  и число
и число  такие, что
такие, что
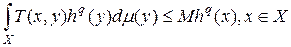 (14)
(14)
и
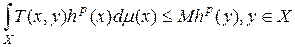 , (15)
, (15)
где 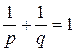 , то оператор
, то оператор  является ограниченным оператором на
является ограниченным оператором на 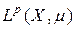 , причём
, причём 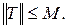
Доказательство. Фиксируем функцию 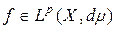 . Используя неравенство Гёльдера, имеем:
. Используя неравенство Гёльдера, имеем:

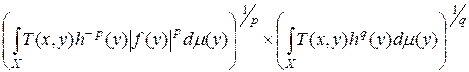 .
.
С помощью неравенства (14) получаем
 .
.
Откуда
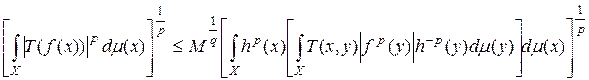 .
.
Теперь, применяя теорему Фубини и меняя порядок интегрирования, получаем:
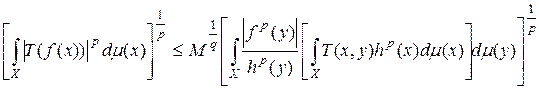 .
.
Далее, учитывая неравенство (15), окончательно выводим:
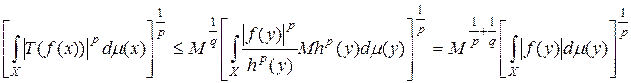 то есть
то есть 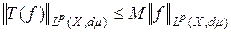 . □
. □
Теорема 8.Пусть 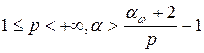 , тогда оператор
, тогда оператор
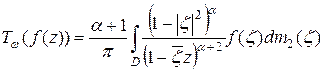 (16)
(16)
отображает пространство 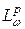 на пространство
на пространство 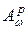 .
.
Доказательство. Утверждение о том, что каждая функция из класса 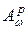 допускает представление (16), непосредственно следует из теоремы 4.
допускает представление (16), непосредственно следует из теоремы 4.
Остаётся установить, что при каждой 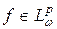 функция
функция 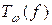 принадлежит классу
принадлежит классу 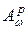 . Докажем указанное утверждение сначала при
. Докажем указанное утверждение сначала при 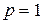 . Из равенства (16) имеем:
. Из равенства (16) имеем:
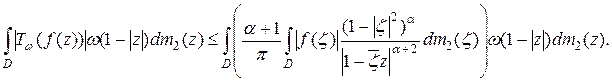 Изменив порядок интегрирования, получили:
Изменив порядок интегрирования, получили:

Теперь, учитывая лемму 1, имеем:
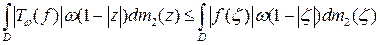 .
.
Теорема доказана при 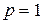 .
.
Теперь предположим 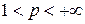 . В этом случае применим теорему 7 и лемму 1. Докажем, что если
. В этом случае применим теорему 7 и лемму 1. Докажем, что если
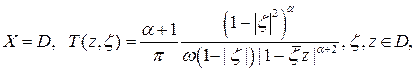 ,
,
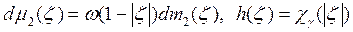 , то все условия теоремы выполнены.
, то все условия теоремы выполнены.
Действительно, условия (14), (15) непосредственно следуют из неравенств а), б) леммы 1. Следовательно, все условия теоремы 7 выполнены. □
Точно таким же образом устанавливается
Теорема 9. Пусть 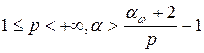 и
и 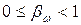 , тогда оператор
, тогда оператор
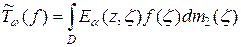
отображает пространство 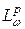 на пространство
на пространство 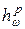 .
.
Следующая теорема играет существенную роль при описании линейных непрерывных функционалы на пространствах 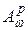 .
.
Теорема 10.Пусть 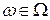 ,
, 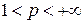 ,
, 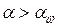 . Тогда оператор
. Тогда оператор
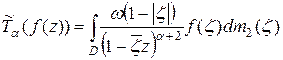 ,
, 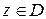 ,
,
отображает пространство 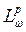 в пространство
в пространство  где
где 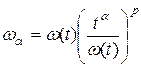 ,
, 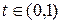 .
.
Доказательство. Как и прежде, положим 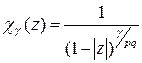 ,
, 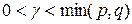 ,
, 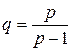 . Тогда, применяя неравенство Гёльдера, получим:
. Тогда, применяя неравенство Гёльдера, получим:
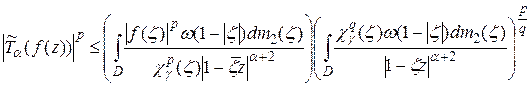 . (2.17)
. (2.17)
По лемме 2.1 отсюда имеем:
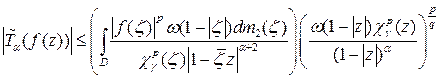 ,
, 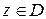 .
.
Умножая последнее неравенство на 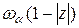 , интегрируя по
, интегрируя по 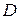 и учитывая последнюю оценку, выводим:
и учитывая последнюю оценку, выводим:
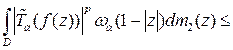
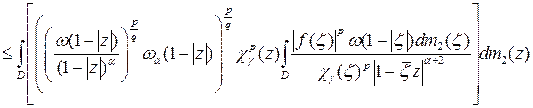 .
.
Преобразуя подынтегральное выражение первого интеграла, получим:
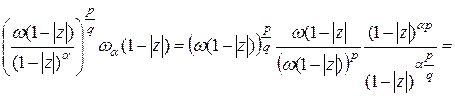
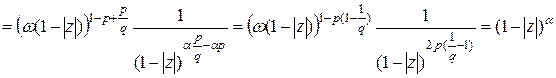 ,
,  .
.
Поэтому из оценки (2.17) имеем:
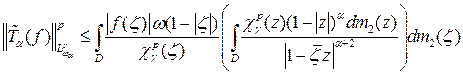 .
.
Снова используя лемму 2.1, окончательно получаем:
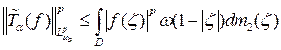 . □
. □
5. Оценки гармонически сопряжённых функций в 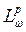 -пространствах при
-пространствах при 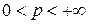
Знаменитая теорема М. Рисса утверждает, что если 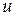 и
и 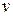 – взаимно сопряжённые гармонические функции, причём
– взаимно сопряжённые гармонические функции, причём  , то при
, то при 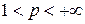 справедлива оценка
справедлива оценка 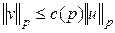 , где
, где

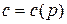 зависит только от
зависит только от 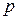 , причём
, причём 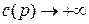 , если
, если 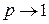 или
или 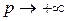 .
.
В этом параграфе нас интересует аналог оценки М. Рисса в 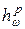 -пространствах.
-пространствах.
Ясно, что при 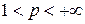 из теоремы М. Рисса непосредственно следует
из теоремы М. Рисса непосредственно следует 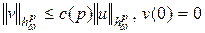 . Однако хорошо известно, что, несмотря на это, при
. Однако хорошо известно, что, несмотря на это, при 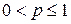 соответствующая оценка неверна.
соответствующая оценка неверна.
Мы докажем, что оператор гармонического сопряжения 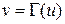 является ограниченным в
является ограниченным в 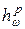 при всех
при всех 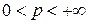 .
.
Лемма 2. Пусть 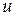 – гармоническая функция в некотором круге
– гармоническая функция в некотором круге 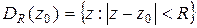 и
и 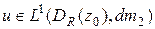 . Тогда при всех
. Тогда при всех 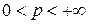 справедлива оценка
справедлива оценка
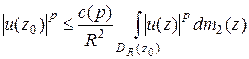 , (18)
, (18)
где 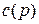 зависит только от
зависит только от 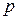 .
.
Доказательство. Если 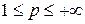 , то оценка непосредственно следует из теоремы о среднем и неравенства Гёльдера. Остаётся доказать лемму при
, то оценка непосредственно следует из теоремы о среднем и неравенства Гёльдера. Остаётся доказать лемму при 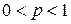 . Не ограничивая общности, можно предположить, что
. Не ограничивая общности, можно предположить, что 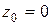 , а
, а 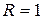 . Как и прежде, обозначим через
. Как и прежде, обозначим через 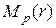 интегральные средние от функции, то есть
интегральные средние от функции, то есть
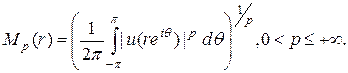
Не ограничивая общности, будем предполагать также, что
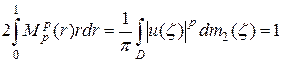 .
.
В этих предположениях, если при некотором 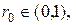
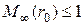 , то лемма будет следовать из принципа максимума, при этом
, то лемма будет следовать из принципа максимума, при этом 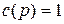 .
.
Поэтому будем предполагать, что 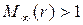 при всех
при всех 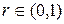 . Поскольку
. Поскольку 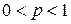 , то
, то
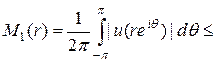
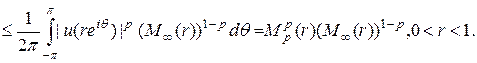
Записывая представление Пуассона для функции 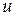 по окружности
по окружности 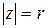 , получаем:
, получаем:
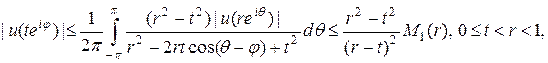
то есть
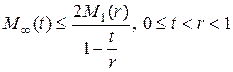 . (19)
. (19)
Пусть теперь  – произвольное число, такое, что
– произвольное число, такое, что  . Тогда из оценки (19) непосредственно имеем:
. Тогда из оценки (19) непосредственно имеем:
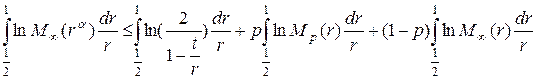 .(2.20)
.(2.20)
Первый интеграл, очевидно, сходится и равен некоторой константе 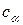 . Оценим второй интеграл в (20). Ясно, что
. Оценим второй интеграл в (20). Ясно, что
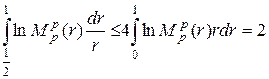 .
.
Следовательно, из неравенства (19) получаем:
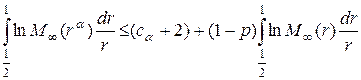 . (21)
. (21)
Поскольку по предположению 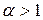 ,
, 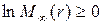 , то
, то
 .
.
Но заменив 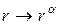 , последний интеграл можно записать в виде
, последний интеграл можно записать в виде
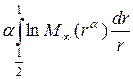 .
.
Следовательно, неравенство (21) преобразуется в
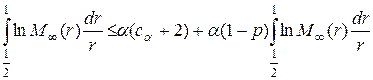 .
.
Теперь подбирая параметр 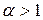 таким образом, чтобы
таким образом, чтобы 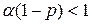 , из последней оценки получаем:
, из последней оценки получаем:
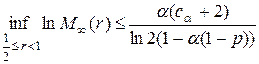 ,
,
то есть
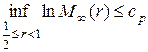 .
.
Тогда неравенство (18) следует из принципа максимума. Что и требовалось доказать. □
Лемма 3. Пусть 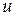 – гармоническая функция в
– гармоническая функция в 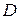 такая, что
такая, что
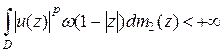 ,
,
то есть 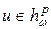 ,
, 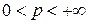 . Тогда
. Тогда
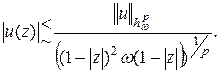
Доказательство. Пусть 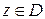 ,
, 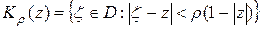 . Применяя лемму 2 к функции
. Применяя лемму 2 к функции 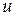 по кругу
по кругу 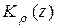 , получим:
, получим:
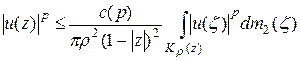 ,
,
Остается положить 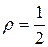 и повторить рассуждения, проведенные при доказательстве теоремы 1. □
и повторить рассуждения, проведенные при доказательстве теоремы 1. □
Лемма 4. Пусть 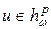 ,
, 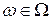 ,
, 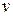 – гармонически сопряженная функция с
– гармонически сопряженная функция с 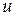 ,
, 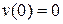 . Тогда при всех
. Тогда при всех 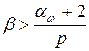 , где
, где 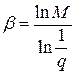 , справедлива оценка
, справедлива оценка
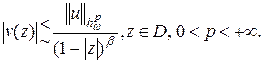 (22)
(22)
Доказательство. Пусть 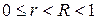 . Тогда имеем
. Тогда имеем
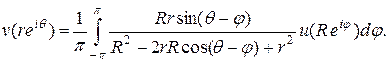
Поэтому
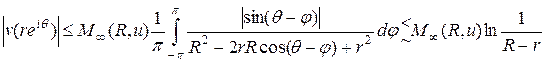 , (23)
, (23)
где, как и прежде, 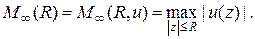
Теперь используя лемму 3, из оценки (23) получим:
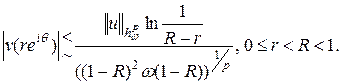
Положим 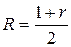 , тогда
, тогда 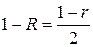 ,
, 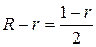 , и поэтому
, и поэтому
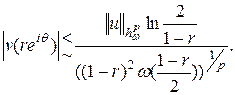
Чтобы получить оценку (2.22), достаточно применить следствие 1.1, согласно которому при всех  ,
, 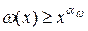 . То есть
. То есть
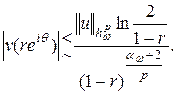
Напомним, что 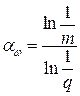 . Из последнего неравенства немедленно следует утверждение леммы. □
. Из последнего неравенства немедленно следует утверждение леммы. □
В дальнейшем существенную роль сыграет следующее диадическое разбиение единичного круга 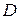 . Пусть
. Пусть 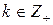 , где
, где 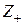 – множество неотрицательных целых чисел,
– множество неотрицательных целых чисел,
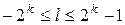 ,
, 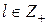 ,
,
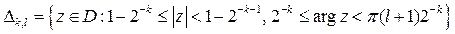 .
.
При этих же  , положим
, положим 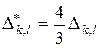 – криволинейный прямоугольник с центром, совпадающим с центром
– криволинейный прямоугольник с центром, совпадающим с центром 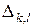 , и расширенный 4/3 раза.
, и расширенный 4/3 раза.
Ясно, что система диадических прямоугольников 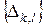 покрывает единичный круг
покрывает единичный круг 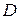 однократно, причем
однократно, причем 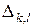 и
и 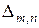 пересекаются только, возможно, границами, если
пересекаются только, возможно, границами, если 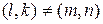 . Система
. Система 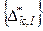 покрывает
покрывает 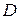 конечнократно.
конечнократно.
Справедливо следующее утверждение:
Теорема 10.Пусть 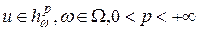 . Тогда справедлива оценка
. Тогда справедлива оценка
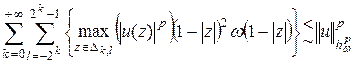 .
.
Доказательство. Сначала установим оценку
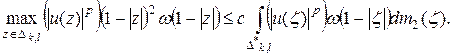 (24)
(24)
Пусть  – произвольная точка из
– произвольная точка из 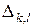 ,
, 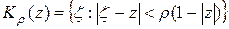 ,
, 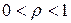 . Тогда из леммы 2.3 имеем:
. Тогда из леммы 2.3 имеем:
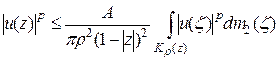
или
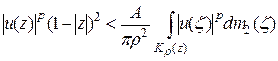 .
.
Положив 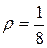 и заметив, что при всех
и заметив, что при всех 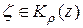
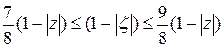 ,
,
по теореме 2.1 будем иметь:
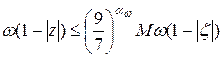 ,
,
откуда приходим к оценке
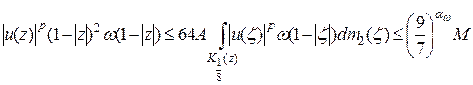 .
.
Учитывая последнее неравенство, в итоге получаем:
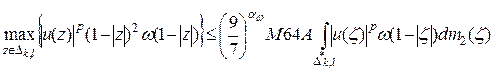 . (25)
. (25)
В неравенстве (25) мы учитывали, что 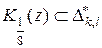 для произвольного
для произвольного 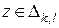 . Суммируя неравенства (25) по
. Суммируя неравенства (25) по 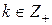 и
и 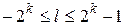 , выводим:
, выводим:
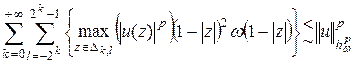 ,
, 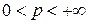 ,
, 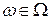 .
.
Здесь мы учли, что последовательность 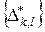 покрывает
покрывает 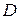 конечнократно. □
конечнократно. □
Теорема 11.Пусть 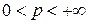 ,
, 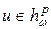 ,
, 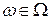 ,
, 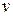 – гармонически сопряженная функция с
– гармонически сопряженная функция с 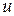 . Тогда
. Тогда
а) 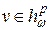 , и если
, и если 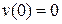 , то
, то
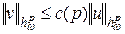 ,
, 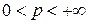 .
.
б) Если 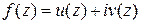 ,
, 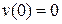 , то линейный интегральный оператор
, то линейный интегральный оператор
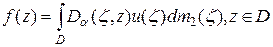 ,
,
при всех 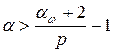 отображает
отображает 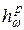 на
на 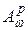 . При этом
. При этом
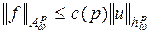 ,
, 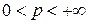 .
.
Доказательство. Сначала заметим, что если 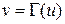 , где
, где 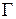 – оператор гармонического сопряжения, то по лемме 2.4
– оператор гармонического сопряжения, то по лемме 2.4 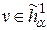 при
при 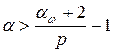 , где
, где 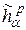 совпадает с
совпадает с 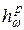 при
при 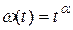 ,
, 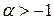 . Этому же классу принадлежит функция
. Этому же классу принадлежит функция 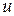 . Поэтому функция
. Поэтому функция 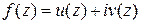 принадлежит классу
принадлежит классу 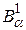 .
.
Следовательно, доказательство теоремы сводится к установлению пункта б). Учитывая теорему 4 и формулу (7), получаем:
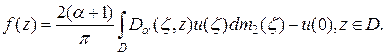
Не ограничивая общности, можно предположить, что 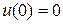 , поскольку очевидно, что
, поскольку очевидно, что 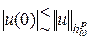 ,
, 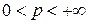 ,
, 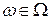 .
.
Далее заметим, что утверждение б) при 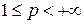 непосредственно следует из теоремы 8. Поэтому в дальнейшем будем предполагать, что
непосредственно следует из теоремы 8. Поэтому в дальнейшем будем предполагать, что  . Ясно, что
. Ясно, что
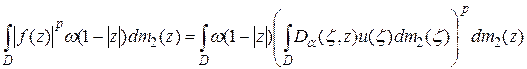 .
.
Следовательно, учитывая, что  , получаем:
, получаем:
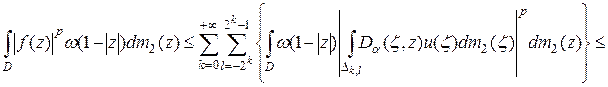
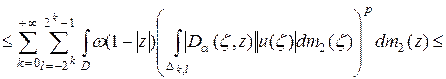
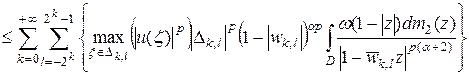 , (2.26)
, (2.26)
где 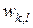 – центр прямоугольника
– центр прямоугольника 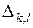 ,
, 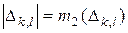 .
.
Теперь оценим последний интеграл 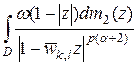 . Используем лемму 1, согласно которой
. Используем лемму 1, согласно которой
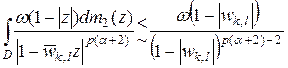 ,
,
если 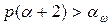 , то есть
, то есть 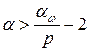 .
.
Следовательно, из (26) получаем:
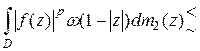
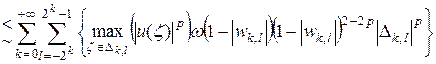 . (27)
. (27)
Теперь заметим, что согласно неравенствам (3)
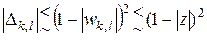 ,
, 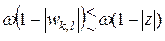 ,
,
для произвольного 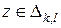 ,
, 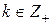 ,
, 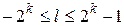 .
.
Учитывая неравенство (27), окончательно имеем:
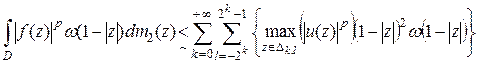 .
.
По теореме 10 последняя сумма не превосходит 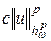 . □
. □
Из этой теоремы непосредственно следует
Теорема 12.Пусть 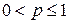 ,
, 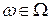 . Тогда следующие утверждения равносильны:
. Тогда следующие утверждения равносильны:
а) 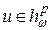 ;
;
б) 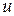 допускает представление
допускает представление
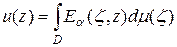 ,
, 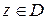 ,
,
где 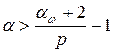 ,
, 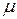 – комплекснозначная борелевская мера, для которой
– комплекснозначная борелевская мера, для которой
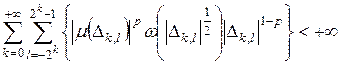 .
.
Доказательство. Вначале докажем импликацию а) 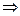 б). Если
б). Если 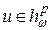 , то согласно теореме 6
, то согласно теореме 6 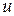 допускает представление (11), где
допускает представление (11), где 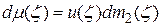 .
.
Согласно теореме 10 мера 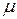 удовлетворяет условию (24). Чтобы установить импликацию б)
удовлетворяет условию (24). Чтобы установить импликацию б)  а) достаточно повторить вторую часть доказательства теоремы 11. □
а) достаточно повторить вторую часть доказательства теоремы 11. □
Аналог теоремы 12 для случая 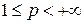 непосредственно следует из теоремы 8, а именно:
непосредственно следует из теоремы 8, а именно:
Теорема 13.Пусть 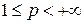 ,
, 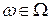 ,
, 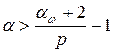 . Тогда следующие утверждения равносильны:
. Тогда следующие утверждения равносильны:
а) 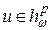 ;
;
б) 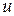 допускает интегральное представление
допускает интегральное представление 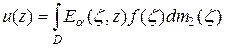 , где
, где 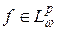 .
.
Дата добавления: 2015-08-14; просмотров: 1694;
