Формула для гармонически спряженной функции
Предположим, что
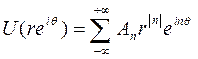 ,
, 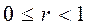
тогда
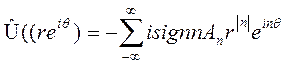
где, sign 0=0
В самом деле, функция Û(reiѲ) гармонична в единичном круге, Û(0)=0
Кроме того
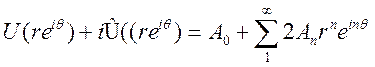
аналитическая функция в единичном круге
Теперь, если

где 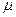 мера на [-π;π], то в вышеприведенном разложении функции U в ряд
мера на [-π;π], то в вышеприведенном разложении функции U в ряд 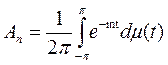 . Рассматривая разложение в ряд для Û, видим, что
. Рассматривая разложение в ряд для Û, видим, что
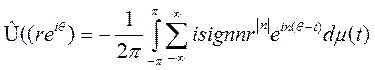
назовем
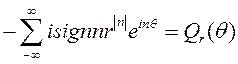
сопряженным ядром Пуассона. непосредственным суммированием двух геометрических прогрессий найдем, что
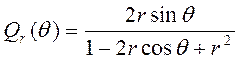
Таким образом справедлива теорема
Теорема Если 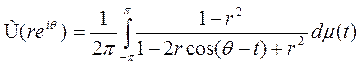 , то гармонически спряженная U функция Û задается формулой
, то гармонически спряженная U функция Û задается формулой
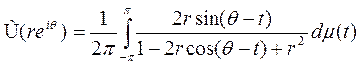
Интегральное представление классов 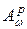
Важную роль в изучении классов 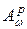 играет интегральное представление функций из этих классов.
играет интегральное представление функций из этих классов.
Сначала докажем следующее утверждение:
Теорема .Пусть 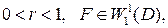 где
где 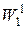 – класс Соболева в
– класс Соболева в 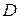 . Если при этом существует такое число
. Если при этом существует такое число 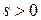 , что
, что 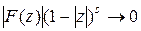 и
и 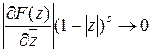 при
при 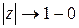 , то при всех
, то при всех 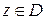 справедливо представление
справедливо представление
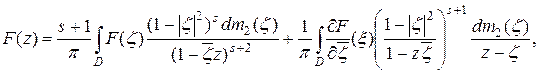 (2.5)
(2.5)
где, как обычно, 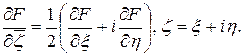
Доказательство. Пусть 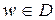 фиксировано, положим
фиксировано, положим
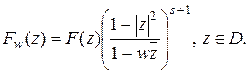 Тогда, записав формулу Коши-Грина для функции
Тогда, записав формулу Коши-Грина для функции 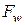 (см. [31]), имеем:
(см. [31]), имеем:
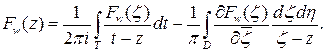
Используя условие теоремы, получаем:
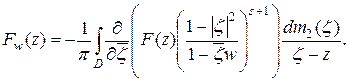
Упростим подынтегральное выражение:
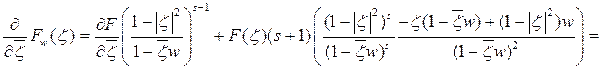
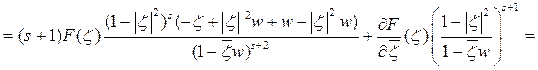
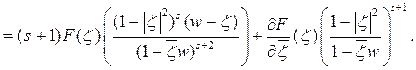
Следовательно, из равенства (2.5) имеем:
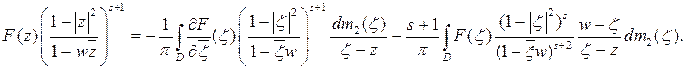
Положив  , получаем:
, получаем:
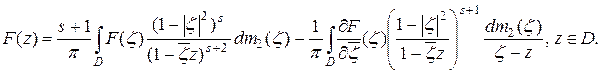 □
□
Из данной теоремы непосредственно следует:
ТеоремаПусть 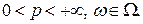 . Тогда если
. Тогда если 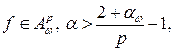 или
или 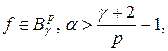 то справедливо представление
то справедливо представление
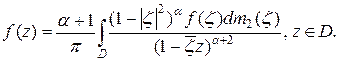
Доказательство непосредственно следует из теоремы 2.3, если учесть, что 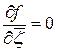 , при этом в условиях теоремы
, при этом в условиях теоремы 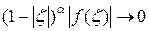 при
при 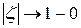 .
.
□
Из интегрального представления классов 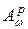 вытекает:
вытекает:
Теорема. Пространство 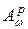 при
при 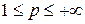 относительно нормы
относительно нормы
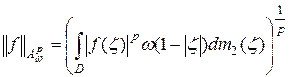
является банаховым, а при 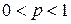 – квазибанаховым пространством.
– квазибанаховым пространством.
Доказательство. Пусть 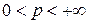 . Обозначим через
. Обозначим через 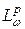 пространство измеримых в
пространство измеримых в 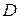 функций
функций 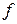 , для которых соответствующий интеграл конечен.
, для которых соответствующий интеграл конечен.
Хорошо известно, что пространство 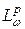 при
при 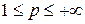 банахово, а при
банахово, а при 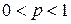 квазибанахово. Поэтому достаточно установить, что
квазибанахово. Поэтому достаточно установить, что 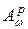 является замкнутым подпространством пространства
является замкнутым подпространством пространства 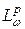 при всех
при всех 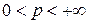 .
.
Предположим, что 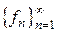 – последовательность из
– последовательность из 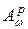 , а функция
, а функция 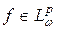 такая, что
такая, что 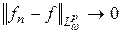 при
при 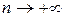 .
.
Докажем, что 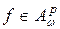 . Используя оценку (2.1), имеем:
. Используя оценку (2.1), имеем:
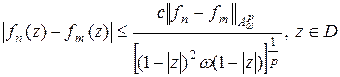 .
.
Отсюда следует, что последовательность 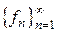 равномерно сходится внутри
равномерно сходится внутри 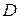 к некоторой функции
к некоторой функции 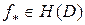 . Учитывая теорему Ф. Рисса (см. [17]), нетрудно подобрать подпоследовательность
. Учитывая теорему Ф. Рисса (см. [17]), нетрудно подобрать подпоследовательность 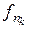 такую, что
такую, что 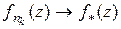 почти всюду в
почти всюду в 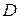 . Поэтому
. Поэтому 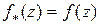 почти всюду в
почти всюду в 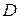 , и следовательно,
, и следовательно, 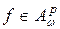 . □
. □
Дата добавления: 2015-08-14; просмотров: 720;
