Классы Нр 0 < р < ∞. Факторизация

Определение Если р > 0, то пространство Н^р состоит нз функций F(z) аналитических в {|z|< 1}, для которых

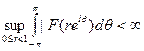(1)

Теорема Если 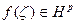р>0, и 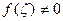, то в ζ|<1 имеем

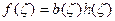(2)

где b(ζ)—функция Бляшке, a 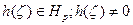в ζ|<1

Доказательство.

Покажем сначала, что интеграл (6.1) есть неубывающая функция от r в 0<r<1. Действительно, при любом фиксированном ρ, 0 <ρ < 1, функция 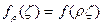регулярна в 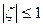и, следовательно, имеет в ζ|<1 представление:

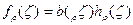
где

b_ρ(ζ)—функция Бляшке, a 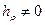в ζ|<1 Функция {h_p(ζ)}^p регулярна в 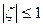; следовательно, из примененной к ней формулы

Пуассона имеем в ζ|<1:

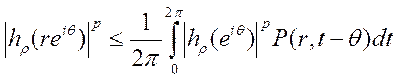
Интегрируя это неравенство по Ѳ от 0 до 2π, получаем:

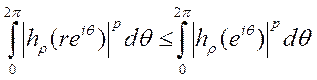(3)

Но так как 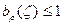в ǀζ|<1 и 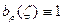на ǀζ|=1, то 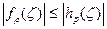в ǀζ|<1 и 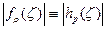на ǀζ|=1, следовательно, имеет место неравенство:

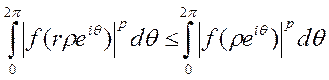
доказанное, таким образом, при любых r и ρ из 0<r<1. Заменяя здесь r на ρ'/ρ, ρ'<ρ, и получим неравенство, доказывающее неубывание интеграла (6.1) в 0<r<1.

Обращаясь теперь к доказательству теоремы, отметим, что в ǀζ|<1 имеет место представление (2) с функцией h(ζ), регулярной и без нулей в ǀζ|<1 . Докажем, что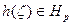

Пусть верхняя граница интегралов (1) в 0<r<1 равна М.

Обозначив через b_n (ζ) произведение n первых множителей в представлении

(*)

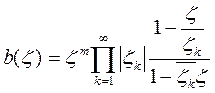функции Бляшке b (ζ) и выбирая для заданного ε, 0<ε<1, и фиксированного п такое η>0, чтобы в ǀζ|>1-η было ǀb_n (ζ)ǀ > 1- — s, что возможно, при 1 — η <r < 1 имеем:

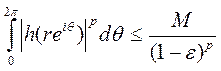(4)

Но так как интеграл в (4) есть неубывающая функция от r 0<r<1, то неравенство (4) имеет место и при 0<r<1—η, т. е. во всем промежутке 0<r<1. Фиксируя r и устремляя n k ∞, из (4) получаем при 0<r<1, учитывая еще произвольность ε>0:

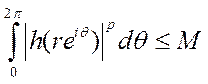
Это и доказывает, что 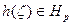и даже более, что верхние границы интегралов (1) для f(ζ) и для h(ζ) в промежутке 0<r<1 будут равны.

Теорема доказана.

Следствие. Если 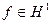, то мы можем найти такие две функции g и h, принадлежащие Н ¹ что и не имеющие нулей в {|z|<1}, что

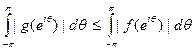
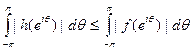
и f=g+h

Замечание. Этот технический результат оказывается часто полезным, так как многие неравенства для функций из Н¹ легче доказывать для функций, не имеющих нулей в {|r|<1}.

Доказательство

Пусть В (r)—произведение Бляшке, построенное по нулям функции f(z). Тогда по предыдущей теореме f= BF, где F(z) не имеет нулей в {|z| < 1}, 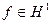и

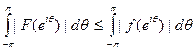
Мы получаем требуемый., результат, полагая

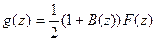
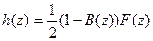
поскольку, как непосредственно проверяется (или же следует из строгого принципа максимума), |В(z)\<1 для |z|< 1.

Следствие. Пусть функция 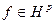, Тогда её можно предста­вить в виде

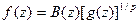
где В (z) — произведение Бляшке, а функция g принадлежит H¹ и не имеет нулей в {|z|<1}.

Доказательство.

Функция f(z) допускает представление f=BF, где функция 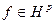не имеет нулей в {|z|<1}. Положим g(z) = [F(z)]^p для |z|< 1. Тогда функция g(z) одно­значна н регулярна в круге {|z|<1}, поскольку F нигде нём не обращается в нуль.