Вероятность появления хотя бы одного из событий.

Пусть в результате опыта может появиться n-событий A₁, A₂,¼,A_n в независимой совокупности, либо некоторое из них. Вероятности появления каждого из событий известны.

Теорема.

Вероятность появления хотя бы одного из событий A₁, A₂,¼,A_n в независимой совокупности равна разности между единицей и произведением вероятностей событий.

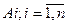
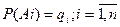
Доказательство:

Пусть A- событие , состоящее в появлении хотя бы одного из событий . Рассмотрим события как .

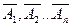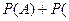
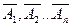)=1

По теореме умножения вероятность произведения равна произведению вероятностей.

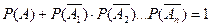
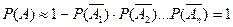
Пусть событие имеет одинаковую вероятность равную P, тогда вероятность появления хотя бы одного события имеет вид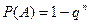

Пример: Два орудия ведут стрельбу по мишени . Вероятность попадания в точке для 1-го орудия -0,5, для второго-0,4. Найти вероятность хотя бы одного попадания в точке, если из каждого орудия сделано по 3 выстрела.

Решение: Пусть событие A₁-попадание из 1-го орудия при одном выстреле;

A₂- попадание из 2-го орудия при одном выстреле, найдем .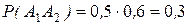

Событие B -хотя бы одно попадание в мишень при 3-х выстрелах из обоих орудий.

P(B)=1-(0,3)³=1-0,027=0,973.