Повторение опытов.

Схема Бернулли.

При практическом применении теории вероятности часто приходится встречаться с задачами, в которых один и тот же опыт или аналогичные опыты повторяются неоднократно. В результате каждого опыта может появиться или не появиться некоторое событие A , причем нас интересует не результат каждого отдельного опыта, а общее число появлений события A в результате серии опытов.

Например: если производится группа выстрелов по одной и той же цели , нас, как правило, интересует не результат каждого выстрела, а общее число попаданий.

В подобных задачах требуется уметь определять вероятность любого заданного числа появлений события в результате серии опытов.

Также задачи решаются весьма просто в случае, когда опыты являются независимыми ( т.к. при этом легко вычисляется вероятность появления события A).

Опыты независимы, если вероятность того или иного результата в каждом из них не зависит от исходов других опытов. Независимые опыты могут производиться в одинаковых или не одинаковых условиях. Мы рассматриваем лишь такие опыты, в которых событие A имеет одну и ту же вероятность.

Задача.

Пусть производиться n-независимых опытов, в каждом из которых событие A может появиться с вероятностью p, требуется определить вероятность того, что событие A в этих n-опытах появиться ровно m-раз.

Искомую вероятность обозначим как P_n(m). Рассмотрим сначала частный случай.

n=3,m=2;

Ai -появление события в i-опыте.

- не появление события в i-опыте.

Возможные исходы опыта можно описать схемой, где приведем вероятности различных исходов.

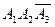
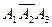
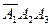
ppq	pqp	qpp
	p2q

Интересующее нас событие сложное- это сумма всех других случаев. Ai- p; - q.

B= + +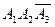

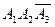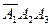
Все слагаемые справа несовместны, поэтому вероятность от суммы будет равна сумме вероятности.

B= 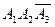+ + 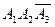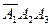=3p²q

Рассмотрим общий случай , когда событие появится m-раз. Интересующее нас событие p распадается на сумму несовместных событий, состоящее каждое в том , что в определенных m-опытах , происходит событие A, а в остальных n-m опытах, событие A не происходит, т.е. . Число всех возможных схем из n-элементов , в которых m-раз встречается событие A в различном порядке равно числу сочетаний 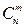. Т.к. оно равно находится числу способов

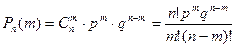-Формула Бернулли или схема Бернулли.

Задача.

Ожидается прибытие 3-х судов с фруктами, статистика показывает , что 1% фруктов груз портится в дороге, найти вероятность того, что прейдет с порченным грузом 1 судно.

n=3, m=1, p=0,01; q=1-0,01=0,09

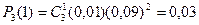
Формулой Бернулли практически невозможно пользоваться , если число испытаний большое, т.к. необходимо вычислять факториалы больших цифр. В случае произведение npq³1, т.е. в этих случаях используют теорему Лапласа.

Существует локальная и интегральная теорема Лапласа.