Интегральная теорема Лапласа.
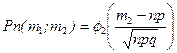 -
- 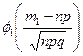 ;
; 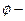 можно найти по таблице в учебнике.
можно найти по таблице в учебнике.
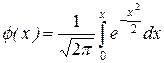 ;
;
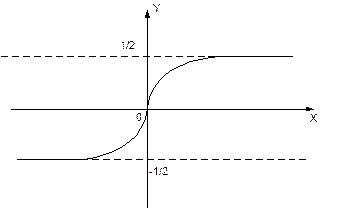 |
Функция Лапласа не выражается через элементарные функции, это функция монотонно возрастающая, нечетная.
Случайные величины.
Понятие случайной величины является одним из центральных понятий теории вероятности.
Случайной величиной называется величина , которая в данном опыте может принять то или иное значение, причем неизвестно заранее какое именно.
Приведем некоторые примеры случайных величин
1. Число выстрелов, производимых до первого попадания в цель.
2. Расстояние от центра мишени до точки попадания .
3. Число бракованных деталей в партии из N изделий.
4. Число шайб , заброшенных в ворота.
5. Ошибка измерения.
Несмотря на всю разнородность приведенных примеров , все они с точки зрения математики представляют одну и ту же картину. А именно , в каждом примере мы имеем дело с величиной, которая под влиянием случайных обстоятельств способна принимать различные значения.
Заранее указать, какое значение примет эта величина, нельзя, т.к. оно меняется случайным образом от опыта к опыту.
Случайные величины обозначают большими буквами, а их значения малыми x, y…. В отличие от переменных величин х1, х2,… случайные величины меняют значения даже при неизменных условиях опыта. Между случайными величинами и событиями существует связь. Понятие случайной величины - общее всякое событие можно истолковать как случайную величину, принимающую только два значения:
0 – если событие не появляется;
1 – если событие появляется.
Различают случайные величины дискретного и непрерывного типа.
Дискретной величиной (прерывной) – называется случайная величина, которая принимает отдельные изолированные, возможные значения с определенными вероятностями. Непрерывной называется случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
Дата добавления: 2015-08-14; просмотров: 637;
