Свойства функций распределения

1. Функция F(х) – не убывающая функция, при х₂³х₁, следовательно F(х₂)³F(х₁).

Доказательство: пусть Х – случайная величина. Х₁ и Х₂ – две произвольные точки, причем х₁<х₂. Сравним значение функции в этих точках. Так, как событие Х<x₁ влечет за собой Х<x₂, то вероятность также будет

Р(Х<x₁)£Р(Х<x₂)

F(x₁)£F(x₂)

2. Значение функции распределения принадлежит промежутку [0;1]. Свойство вытекает из определения 0£F(x)£1, вероятность - есть неотрицательное число, не превышающее единицы.

3. Если возможные значения случайной величины принадлежат промежутку (a;b), то значение функции распределения равно нулю, если х<а равно 1, то F(х)=0 и F(х)=1, если х>b,

F(х)=0 х<а

F(х)=1 х>b

Доказательство.

1) Пусть х₁£а, тогда событие X<х₁ – невозможно, т.к. значения меньших х₁ , величина х по условию не принимает, следовательно его вероятность равна 0.

2) Пусть х₂³b, тогда событие X<х₂ достоверно, т.к. все возможные значения X<х₂, следовательно вероятность такого события равна 1.

Следствие: если возможные значения непрерывной случайной величины расположены на всей оси ox, то справедливо следующее соотношение.

;

.

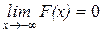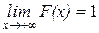График функции распределения в общем случае представляет собой график неубывающей функции, значение которой начинаются от нуля и доходят до 1. Причем в отдельных точках функция может иметь разрывы.

Для дискретной случайной величины график F(х) имеет ступенчатый вид.

Пример:

Два стрелка сделали по выстрелу в мишень . Вероятность попадания первого в мишень равна 0,6, для второго 0,8. Составить таблицу распределения и построить ее график.

Обозначим x-число попаданий в мишень, тогда x принимает значения:

A₁-попал первый; 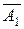-не попал первый;

A₂- попал второй; 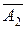-не попал второй,

;

;

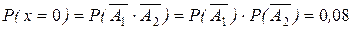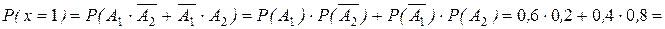
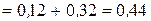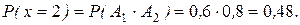
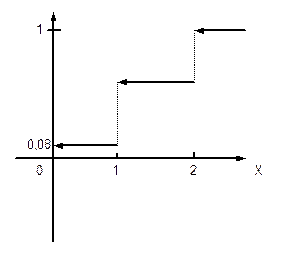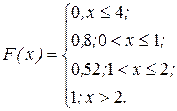
Вероятность попадания случайной величины в пределы заданного участка.

Зная функцию F(x) , вычислим вероятность того, что случайная величина примет значение заключенное в интервале (a;b). Пользуясь теоремой сложения вероятностей запишем вероятность того, что х<b будет складываться из вероятностей Р(х<b)=Р(х<a)+Р(а£х). Выразим Р(а£х<b)=Р(х<b)-P(x<a)=F(b)-F(a). Таким образом искомая вероятность равна приращению функции распределения на данном интервале.

Отдельная вероятность попадания в точку. Полученную формулу нахождения вероятностей используем для х=а при условии, что

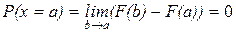
Пример: Случайная величина задана функцией распределения

F(x)=0 x<2;

F(x-2)² 2£x£3;

F(x)=1 x>3.

Вычислить вероятность случайной величины в интервале P(3,5£х£2,5) и Р(1<х<2,5).

P(3,5<x<2,5)=F(3,5)-F(2,5)=1-(2,5-2)²=1-0,25=0,75;

Р(1<х<2,5)=F(2,5)-F(1)=0,25.

Плотность распределения

Непрерывную случайную величину можно задать с помощью плотности распределения вероятностей случайной величины, которая является дифференцируемой функцией распределения. Рассмотрим непрерывную случайную величину x, функция распределения которой непрерывна и дифференцируема.

Определение: плотностью распределения случайной величины x, называют первую производную от функции распределения f(x)=F(x). Установим вероятностный смысл. Из определения производной следует, что это есть предел от приращения функции к приращению аргумента. Разница функций распределения в точке х+Dх, это есть вероятность того, что х попадает в интервал от (х+Dх).

Т.е. плотность распределения случайной величины в точке х, равно пределу отношения вероятности попадания случайной величины х в интервал от х до х+Dх к Dх, когда Dх®0.

Вероятность попадания непрерывной случайной величины в заданный интервал.

Задача.

Зная плотность распределения величины x, вычислим вероятность того, что случайная величина примет значение принадлежащее интервалу от (a;b).

P(a<x<b)=F(b)-F(a)=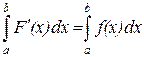

Рассмотрим график плотности распределения.

Кривая распределения имеет вид:

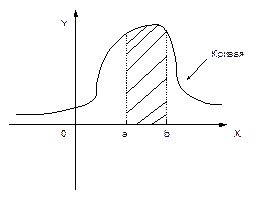Вероятность того, что случайная величина примет значение , принадлежащее интервалу (a;b) равно площади криволинейной трапеции, ограниченной осью ox, кривой распределения f(x) и прямыми х=а, х=b. График функции y=f(x) – называется кривой распределения.

Основные свойства плотности распределения.

1. Функция f(x) неотрицательна f(x)³0, как производная от неубывающей функции.

2. Несобственный интеграл от (-¥; ¥) .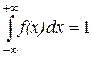

Несобственный интеграл выражает вероятность того, что случайная величина примет значение в интервале (-¥; ¥). Такое событие всегда достоверно, его вероятность равна 1.