Теорема умножения вероятностей.
Вероятность совместного появления 2-х событий равна произведению вероятностей одного из них на словную вероятность другого, вычисленную в предположении, что 1-ое событие уже наступило.
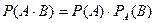
Пусть n-число всех возможных исходов опыта, в котором событие A наступает или не наступает, m-число исходов , благоприятствующих событию A, l- число событий благоприятствующих A×B, в котором событие A уже наступило.
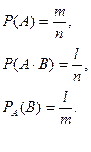
Считаем , что событие A уже наступило, то из раннее возможных n-случаев остаются возможными только те m-которые благоприятствуют событию A , из них l-исходв благоприятствуют событию B.
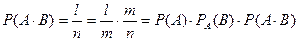
Замечание 1 :
Для независимых событий условная вероятность совпадает с безусловной , поэтому вероятность от произведения равна произведению этих событий.
Замечание 2:
Теорема умножения обобщается на любое число сомножителей при условии, что эти события независимой совокупности.
Несколько событий называются независимыми в совокупности, если вероятность появления одного из них не зависит от того произошли ли какие- либо рассматриваемые события или нет .
Пример:
Студент пришел на экзамен зная 20 вопросов из 25 вопросов. Какова вероятность того, что студент знает каждый из 2-х вопросов, заданных ему экзаменатором?
Пусть событие A- студент знает 1-й вопрос.
B-студент знает 2-й вопрос, тогда вероятность события A,
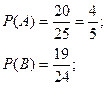 искомая вероятность
искомая вероятность 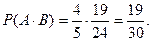
Дата добавления: 2015-08-14; просмотров: 705;
