Полная группа событий.

Совокупность единственно возможных событий опыта называется полной группой событий. Пусть события A₁ , A₂ ,¼ , A_n образуют полную группу .

Следствие : Сумма вероятностей событий , образующих полную группу равна 1.

Доказательство:

Применяя теорему и учитывая , что любые 2 события полной группы несовместны и сумма этих событий - событие достоверное, мы получаем доказываемое следствие.

P(A₁ + A₂+ ¼ + A_n )=1,

P(A₁)+P(A₂)+¼+P(A_n)=1,

Два единственно возможных события , образующих полную группу, называют противоположными.

Противоположными событиями являются например, выпадение герба и выпадение цифры при бросании монеты; попадание и промах при стрельбе в цель; событие "день дождливый" и "день ясный"; события "3 дня подряд шел снег" и " хотя бы в один из 3-х дней снега не было".

Следствие: Сумма вероятностей противоположных событий равна 1.

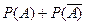=1

Переход к противоположному событию нередко облегчает вычисление вероятности. На практике весьма часто оказывается легче вычислить вероятность противоположного события 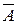, чем вероятность прямого события A. В этих случаях вычисляют вероятность 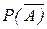, затем находят .

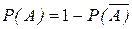Вероятности противоположных событий принято обозначать p и q, следовательно p+q=1.

Пример.

Найти вероятность того, что при стрельбе в мишень , состоящую из центрального круга и 2-х концентрируемых колец, стрелок не попадет в мишень, если он производит 1 выстрел. Вероятности попадания в круг и кольца равна 0,2:0,15=0,1

Пусть событие A- непопадание, - попадание, тогда вероятность попадания равна сумме и равна 0,45, а искомая вероятность равна 1-0,45=0,55.