Сведения из комбинаторики.
1. Если имеется n-элементов одной группы и m-элементов другой группы, то число различных пар , содержащих один элемент из 1-й группы и 2-й группы равно m∙n.
2. Перестановками из n-элементов называются их соединения, различающиеся друг от друга только порядком, входящих в них элементов.

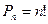
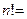 1×2×3×¼×n
1×2×3×¼×n
Возьмем элементы A, B, C
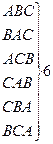
Размещением из n-элементов по m 
 называются такие множества, которые различаются друг от друга, самими элементами или их порядками.
называются такие множества, которые различаются друг от друга, самими элементами или их порядками.
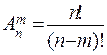
Сочетаниями из n- элементов по m 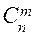 (
( 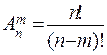 разделить на m! ) называются такие их соединения , которые различаются друг от друга самими элементами.
разделить на m! ) называются такие их соединения , которые различаются друг от друга самими элементами.
Статистическое определение вероятности.
В различных приложениях теории вероятности в естественно- научных и технических вопросах часто пользуются так называемым статистическим определением вероятности.
Допустим имеется возможность неограниченного опыта, в каждом из которых проявляется появление или не появление некоторого события, тогда отношение 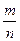 -называют относительной частотой события.
-называют относительной частотой события.
При очень большом числе опытов частота сохраняет почти постоянную величину, причем колебания ее становятся тем меньше , чем больше число опытов. Поэтому вероятностью события называют числовую характеристику, около которой колеблется частота появления события, при сохранении неизменных условий опыта.
Для примера рассмотрим результаты, полученные некоторыми экспериментами при бросании монеты:
| Экспериментатор | Число бросаний | Число выпадение герба | Частота |
| Бюффон К.Пирсон К.Пирсон | 0,5080 0,5016 0,5005 |
Как видно из таблицы , частота здесь приближается к числу 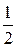 (т.е. вероятность появления герба равна
(т.е. вероятность появления герба равна 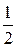 ).
).
Статистическое определение вероятности не является достаточно строгим с точки зрения математики; из него даже не видно, всякое ли случайное событие имеет вероятность . Однако статистическое определение вероятности является самым широким по числу охватываемых событий.
Пример:
Для установления уровня знаний учащихся по математике в пяти восьмых классах различных школ города была проведена контрольная работа, состоящая из 3-х вопросов. Из 200 учащихся , писавших работу , на 1-й вопрос дали верный ответ 180 учащихся , на 2-й -125 и на 3-й- 145. Какой следует считать вероятность того, что наудачу выбранный учащийся 8-го класса городской школы верно ответит на наудачу выбранный вопрос из контрольной работы?
Решение: На все вопросы получено верных ответов =180+125+145=450 ответов; всего ответов=200×3=600 ответов. Следовательно, P= 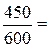
 .
.
Дата добавления: 2015-08-14; просмотров: 830;
