Классическое определение вероятности. Предсказать результат единичного опыта можно лишь для достоверных и невозможных событий
Предсказать результат единичного опыта можно лишь для достоверных и невозможных событий. Случайность же события вообще не видна при единичном опыте: если событие произойдет, оно может показаться нам достоверным, если не произойдет- невозможным.
Теория случайных событий может появиться лишь при большом числе опытов, лишь для массовых событий.
Важным условием при этом является неизменность заданных условий. События, происходящие при одних и тех же условиях , называются однородными.
Практика показывает , что события, сами по себе случайные , в большой массе при наличии однородности начинают подчиняться некоторым неслучайным закономерностям. Эти закономерности получили название вероятностных , а наука, изучающая вероятностные закономерности - теорией вероятности.
Пусть производится некоторый опыт, допустимые результаты опыта назовем элементарными исходами. Пусть эти исходы равновозможны, несовместны и единственно возможны. Обозначим число всех исходов через n , тогда в силу равновозможности исходов возможность проявления каждого из них можно положить равным как 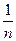 . Те исходы опыта, при которых интересующее нас событие наступает называются благоприятствующими этому событию.
. Те исходы опыта, при которых интересующее нас событие наступает называются благоприятствующими этому событию.
Пусть событие A- интересующее нас событие, а событию A благоприятствует m- исходов , отсюда вопрос, какова возможность появления события A.
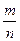 -число(вероятность)
-число(вероятность)
Определение: Отношение числа исходов , благоприятствующих событию A и числу всех несовместных , равномозможных и единственно возможных исходов называют вероятностью события A.
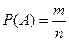 - это число дает количественную оценку возможности появления события A.
- это число дает количественную оценку возможности появления события A.
Свойства.
1. Вероятность достоверного события равна 1. 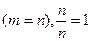 .
.
2. Вероятность невозможного события равна 0.(m=0).
3. Вероятность случайного события есть положительное число, не большее 1.
Вероятность любого события:
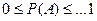
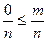 <
< 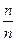 ;
;
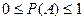 .
.
Задача.
Одновременно бросаются 2 кубика, какова вероятность того, что сумма очков, выпавших на 2-х кубиках равна 8.
Т.к. любое из возможного числа очков на одном кубике может сочетаться на другом, то общее число сочетаний n=36, эти случаи попарно несовместны и равновозможные.
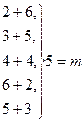 ,
,
Интересующему нас событию благоприятствует 5 случаев
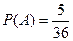 .
.
Дата добавления: 2015-08-14; просмотров: 732;
