Аксиомы статики. В основу статики положено несколько аксиом, полученных в результате многовековых наблюдений и научных обобщений

В основу статики положено несколько аксиом, полученных в результате многовековых наблюдений и научных обобщений. Закон инерции: всякая изолированная материальная точка на- ходится в равновесии, пока какая – нибудь причина не выведет его из чтого состояния. Из этой аксиомы следует понятие силы, как причины, изменяющей состояние покоя пли движения данного тела. В системе СИ за единицу силы принята сила, называемая Ньютоном и обозначаемая Н. О силах судят по их действиям. Эквивалентными считают те силы, которые будучи приложены но отдельности к одному и тому же телу, произведут на его одинаковое действие. Сила - величина векторная, т.к. действие одного тела па другое существенно зависит от направления. Например , если с одной и той же по модулю I силой будем давить сверху вниз на спинку стула, то стул останется в покое, если стул тянут в вверх с силой, больше его веса, го стул будет подниматься, а если силу приложить горизонтально - стул опрокинется. Т.к. во всех Этих случаях действия сил разные, следовательно, и силы разные, несмотря на то, что их модули могут быть одинаковы. Сила, приложенная к твердому телу - вектор несвободный, т.к. ее действие зависит от точки приложения. Например, если не меняя величи­ны силы и ее направления, параллельно полу, потянуть стул за спинку назад, то стул опрокинется, а если потянуть за основание ножки непос­редственно около пола, то стул будет скользить по полу.

Итак, действие силы на твердое тело определяется величиной (модулем), направлением и точкой приложения. Силу, как и другие вектор­ные величины, изображают в виде направленного отрезка. Системой сил называют совокупность нескольких сил, приложенных к матери­альной точке или телу. Если точка или абсолютно твердое тело под действием системы сил находится в равновесии, то такую систему сил называют уравновешенной или эквивалентной нулю.

Простейшая уравновешенная система сил определяется второй аксиомой. Абсолютно твердое тело только тогда находится в равно­весии под действием двух сил, если эти силы равны по модулю и направлены в противоположные стороны по прямой, соединяющей точки приложения этих сил (Рисунок 1. а).

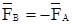_, т.п. по модулю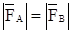

Аксиома третья. Действие системы сил на абсолютно твердое тело не меняется от присоединения или исключения уравновешенной системы сил.

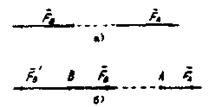
Из приведенных аксиом следует теорема: сила, приложенная к абсолютно твердому телу, является вектором скользящим, т.е. не изме-няя действия силы на абсолютно твердое тело, можно ее прикладывать в произвольной точке по линии действия силы (Рисунок 1. б).

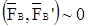В т. А приложена сила , в т.В , причем 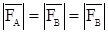по модулю

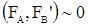
модулю.

Согласно 2 и 3 аксиомам от присо­единения этих сил действие силы не из­менилось, т.е. 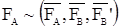. Но согласно аксиоме 2 имеем уравновешен­ную систему

F_A , но только проскользнувшую по линии действия из точки А в точку В.

Итак: действие силы на абсолютно твердое тело определяется модулем, линией действия и направлением силы. Равнодействующей системы сил называют силу, действие которой заменяет собой дей­ствия данной системы сил. Замену одной силы несколькими называют разложением данной силы на составляющие.

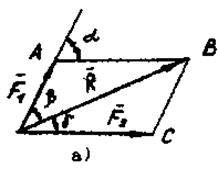
Аксиома четвертая (правило параллелограмма): равнодейству­ющая двух сил, приложенных в точке, приложена в той же точке и равна по величине и направлению диагонали параллелограмма, пост­роенного на этих силах, как на сторонах (Рисунок 2 а). Параллелог­рамм строят в определенном масштабе, т.е. выбранная единица соот­ветствует единице силы.

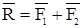
Если силы взаимно перпендикулярны F₁ ^ F₂ , т.е. a=90⁰, согласно

теореме Пифагора имеем: .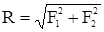

Аксиома пятая (закон действия и противодействия): две мате­риальные точки действуют друг на друга силами, равными по модулю и направленными в противоположные стороны по прямой, соединяю­щей эти точки (Рисунок 2 б).

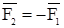
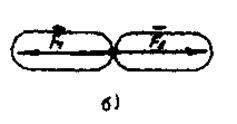
Ньютон так это сформулировал: действие всегда равно и прямо противоположно противодействию:

Рис 2.

Из аксиомы 5 следует, что силы всегда встречаются попарно, т.е. все силы носят характер взаимодействий.

Изменяемой системой материальных точек называют такую со­вокупность точек, в которой расстояния между точками системы мо­гут изменяться. Согласно шестой аксиоме: равновесие изменяемой системы сил не нарушится, если система станет неизменяемой. Де­формируемое тело является изменяемой системой материальных то­чек. Применительно к нему 6-я аксиома носит название принципа от­вердевания: если деформируемое тело находится в равновесии под

действием некоторой системы сил, то равновесие не нарушится, если это тело станет абсолютно твердым. Принцип отвердевания широко используется в инженерных расчетах.