Момент силы и пары. Сила реакции заделки.
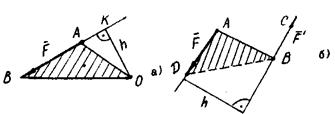
Плечом силы Р относительно точки О называют перпендикуляр ОК. опущенный из точки О на линию действия силы. Моментом силы Р относительно точки О называют алгебраическое значение произведения модуля силы на ее плечо относительно точки О: Mo(F) = ± F·h.
Момент силы относительно точки не меняется при переносе силы по ее линии действия. При вращении плеча под действием силы Р вокруг точки О против часовой стрелки знак момента будет положительный, а при вращении но часовой стрелке - отрицательный.
|
Рис 8.
Момент силы относительно точки О равен нулю, когда сила равна нулю или когда линия ее действия проходит через данную точку.
Из рисунка 8. а видно, что |Mo(F)| = 2 пл DОАВ, т.е. величина момента силы относительно данной точки численно равна удвоенной площади треугольника, основанием которого является сила, а вершиной - данная точка.
Пара - это две равные но модулю, противоположно направленные параллельные силы (Рисунок 8. б). Расстояние h между линиями действия сил пары называют плечом пары. Моментом пары называют алгебраическое значение произведения модуля одной из сил пары на ее плечо:
M(F, F`) = ± Fh
Абсолютное значение момента пары численно равно удвоенной площади треугольника, основанием которого является одна из сил нары, а вершина находится в любой точке на линии действия второй силы пары.
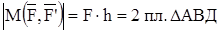
Сумма проекций двух сил, составляющих пару, на какую-либо ось равна пулю. Это очевидно, т.к. проекции сил пары одинаковы по абсолютным величинам и противоположны но знаку.
Пару изображают различным способом (Рисунок 9). Заделка - одна из часто встречающихся связей (опор), как бы один конец балки жестко заделан в стену. Материал стены оказывает на балку реакцию, состоящую из реактивной силы (она представлена в виде двух составляющих сил FA = FX + FY) и реактивной пары, момент которой М называют реактивным моментом или моментом в заделке. Физический смысл реакции в заделке состоит в том. что реактивная пара препятствует повороту балки, обеспечивает жесткость соединения балки со стеной.
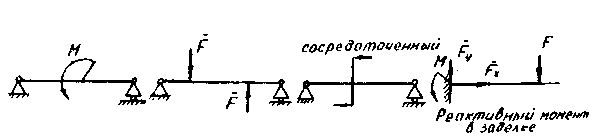
Рис 9.
Момент равнодействующей плоской системы сходящихся сил от-носительно произвольной точки в плоскости сил ранен алгебраической сумме моментов всех составляющих сил относительно той же точки: Mo(FR) = ΣM0(Fx)
Момент равнодействующей системы сходящихся сил относительно какой-либо оси равен алгебраической сумме моментов всех составляющих сил относительно той же оси: 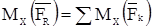 .
.
Дата добавления: 2015-08-08; просмотров: 1848;
