Скорость и ускорение точки

Механическим движением называют изменение с течением вре­мени положения в пространстве точек и тел относительно какого-либо основного тела, с которым скреплена система отсчета. Кинема­тика изучает механическое движение точек и тел независимо от сил, вызывающих эти движения. Всякое движение, как и покой, относи­тельно и зависит от выбора системы отсчета.

Траекторией точки называют непрерывную линию, описывае мую движущейся точкой. Если траектория - прямая линия, то движе­ние точки называют прямолинейным, а если - кривая, то - криволиней­ным. Если траектория - плоская, то движение точки называют плоским.

Движение точки или тела, считается заданным или известным, если для каждого момента времени (t) можно указать положение точ­ки или тела относительно выбранной системы координат.

Положение точки в пространстве определяется заданием:

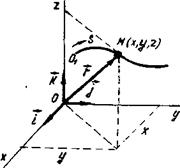
а) траектории точки;

б) начала О₁ отсчета расстояния по траектории (Рису­нок 11): s = О₁М - криволиней­ная координата точки М;

в) направления положи­ тельного отсчета расстояний s;

г) уравнения или закона движения точки по траектории: S = s(t)

Рис 11.

Скорость точки. Если точ­ка за равные промежутки време­ни проходит равные отрезки пути, то ее движение называют равномерным. Скорость равно­мерного движения измеряется отношением пути з, пройденно­го точкой за некоторый проме­жуток времени, к величине это­го промежутка времени: v = s/1. Если точка за равные промежут­ки времени проходит неравные пути, то ее движение называют неравномерным. Скорость в этом случае также переменна и являет­ся функцией времени: v = v(t). Рассмотрим точку А, которая перемещается по заданной тра­ектории по некоторому закону s = s(t) (Рисунок 12):

Рис 12.

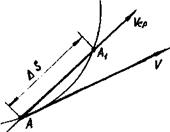
За промежуток времени t т. А переместилась в положение А₁ по дуге АА. Если промежуток времени Δt мал, то дугу АА₁ можно заменить хордой и найти в первом приближении величину средней скорости движения точки v_cp = Ds/Dt. Средняя скорость направлена по хорде от т. А к т. А₁.

Истинная скорость точки направлена по касательной к траекто­рии, а ее алгебраическая величина определяется первой производной пути по времени:

v = limΔs/Δt = ds/dt

Размерность скорости точки: (v) = длима/время, например, м/с. Если точка движется в сторону увеличения криволинейной координаты s, то ds > 0, и следовательно, v > 0, а в противном случае ds < 0 и v < 0.

Ускорение точки. Изменение скорости в единицу времени опреде­ляется ускорением. Рассмотрим движение точки А по криволинейной траектории за время Δt из положения A в положение A₁. В положении A точка имела скорость v , а в положении A₁ - скорость v₁ (Рисунок 13). т.е. скорость точки изменилась по величине и направлению. Геометрическую разность, скоростей Δv найдем, построив из точки A вектор v_1.

Рис 13.

Ускорением точки называют вектора ", равный первой производной от вектора скорости точки по времени:

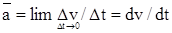
Найденный вектор ускорения а может быть разложен на две взаимно-перпендикулярные составляющие но касательной и нормали к траек­тории движения 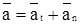. Касательное ускорение а₁ совпадает по на­правлению со скоростью при ускоренном движении или противополож­но ей при замененном движении. Оно характеризует изменение величи-ны скорости и равно производной от величины скорости по времени

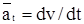
Вектор нормального ускорения а направлен по нормали (пер­пендикуляру ) к кривой в сторону вогнутости траектории, а модуль его равен отношению квадрата величины скорости точки к радиусу кри­визны траектории в рассматриваемой точке.

Нормальное ускорение характеризует изменение скорости по
направлению.

Величина полного ускорения: 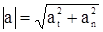, м/с²

Виды движения точки в зависимости от ускорения.

Равномерное прямолинейное движение (движение по инерции) характеризуется тем, что скорость движения постоянна, а радиус кри­визны траектории равен бесконечности.

То есть, r = ¥, v = const, тогда 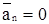; 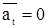и поэтому 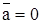. Итак, при движении точки по инерции ее ускорение равно нулю.

Прямолинейное неравномерное движение. Радиус кривизны траектории r = ¥, а_n = 0, поэтому и а = а_t и а = а_t = dv/dt.

Криволинейное равномерное движение. Поскольку v = const, то а_t = dv/dt = 0; 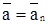= v²/p

Движение точки, при котором величина касательного ускорения постоянна (а_t = соnst) называют равнопеременным. Величину ускоре­ния можно также определить через значение скорости в начале и в конце произвольного промежутка времени t: a_t = (v – v₀)/t, откуда v = v₀ + a_t·t. Путь, пройденный точкой при равнопеременном движении, определится по уравнению:

Примером равномерно-ускоренного движения может служить свободное падение тела, при этом ускорение свободного падения тел вблизи поверхности Земли составляет в среднем g = 9,81 м/с².