Дифференциальные уравнения движения свободной материальной точки.

Спроектируем векторное уравнение 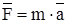на оси координат, учитывая, что проекции вектора ускорения точки на оси координат равны вторым производным по времени от соответствующих координат точки:

m(d²x/dt²) = X; m(d²y/dt²) = Y; m(d²z/dt²) = Z.

Ограничимся случаем, когда движение происходит в плоскости (х, у):

m(d²x/dt²) = X; m(d²y/dt²) = Y

Здесь X, V - проекции на оси координат равнодействующей силы, приложенной к точке. Из кинематики известно, что движение точки может быть задано уравнениями: x = x(t), y = y(t). Масса точки подразумевается известной.

Первой задачей динамики является задача определения силы, если известно движение, вызываемое этой силой. Для нахождения силы (она определяется своими проекциями) нужно дважды продифференцировать каждое из заданных уравнений движения.

Второй, основной задачей динамики является задача определения движения точки под действием заданной силы. В дифференциальных уравнениях движения известны X, Y и, чтобы определить закон движения, нужно систему уравнений проинтегрировать и найти первообразные х и у, причем получаются четыре произвольных постоянных интегрирования:

x = x (t, C₁, C₂, C₃,C₄), y = y (t, C₁, C₂, C₃,C₄),

Эти уравнения движения положения точки не определяют вследствие неопределенности С₁, С₂, С₃, С₄. Следовательно, задание действующих сил недостаточно для определения движения свободной (без связей) материальной точки. Для того, чтобы найти С₁, С₂, С₃, С₄, нужно знать начальные условия, т.е. положение и скорость точки в заданный момент времени t₀ (обычно t₀ = 0). Учитывая, что v_x= dx/dt v_y= dy/dt начальными условиями являются следующие величины:

x₀, y₀, (v_x)₀ = dx/dt)₀, (v_y)₀ = (dy/dt)₀

Имеем четыре условия для определения четырех неизвестных С₁, С₂, С₃, С₄. Итак, движение свободной материальной точки полностью определяется заданием действующих сил и начальных условий. Движение несвободной материальной точки. Принцип освобождаемости от связей. Так же, как и в статике, в динамике имеет место принцип освобождаемости от связей. Несвободную материальную точку или тело, не находящееся в равновесии, можно рассматривать как свободное, если мысленно отбросить связи и заменить их действия силами - динамическими реакциями связей. Второй закон Ньютона, выраженный уравнением F = m · a относится к свободной (без связей) материальной точке. Введенный принцип позволяет распространить этот закон на движение несвободной точки и записать

.

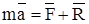
где 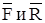- равнодействующие заданных сил и динамических реакций связей. В проекциях получаем

m(d²x/dt²) = X + R_x; m(d²y/dt²) = Y+R_y.

Здесь надо понять, что, решая вторую задачу динамики, т.е. определяя по заданным силам X, V движение точки - уравнения x = x(t), y = y(t) мы сталкиваемся с новыми неизвестными R_X, R_Y.

Но нельзя найти шесть неизвестных величин С₁, С₂, С₃, R_X, R_Y, зная только четыре величины из начальных условий.

Динамические реакции связей по своей природе отличаются от заданных сил, так как они нуждаются в определении и зависят как от заданных сил, так и от характера связей. Итак, движение несвободной материальной точки полностью не определяется заданными силами и начальными условиями. Только задание дополнительных геометрических и физических характеристик (например, идеально гладкие поверхности или заданный коэффициент трения и прочее) позволяют найти по заданным силам и начальным условиям движение несвободной материальной точки.