Принцип Даламбера для материальной точки

Принцип Даламбера в его современном истолковании эквивалентен второму закону Ньютона и принципу освобождаемости от связей, т.е. равнозначен уравнению, но записывается и формулируется в другом виде, удобном для многих приложений. Силой инерции называется вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению:

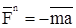; модуль силы: .

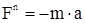Из уравнения 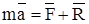находим F + R +(-ma) = 0

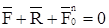
Последнее равенство выражает принцип Даламбера и по своему виду совпадает с необходимым и достаточным условием равновесия системы сходящихся сил: если к заданным силам и реакциям связей, действующим на движущуюся несвободную точку, мысленно добавить силу инерции точки, то получим уравновешанную систему сил. Сила инерции на самом деле к точке не приложена, иначе точка находилась бы в равновесии , а на самом деле она движется с ускорением , т.е. - величина переменная. Применение принципа Даламбера позволяет при решении динамических задач использовать уравнения равновесия. Такой прием решения задач динамики называют методом кинетостатики.