Центр масс. Момент инерции.
Центр тяжести тела определяется формулами, которые были получены при двух предположениях: 1) существуют силы тяжести точек; 2) силы тяжести считаются параллельными.
Однако можно представить себе в пространстве тела, для которых не существует центра тяжести, все точки которых находятся в состоянии невесомости вследствие уравновешивания гравитационных сил (например, тело между Землей и Солнцем в таком месте пространства, в котором притяжения к Земле и Солнцу противоположны по направлению и равны по величине) или вследствие нахождения в неинерциональной системе координат (например, человек в кабине, свободно падающей на Землю, невесом относительно этой кабины). Независимо от центра тяжести существует понятие центра масс как точки, определяемой формулами:
хс = Σmk xk /M yс = Σmk yk /M zс = Σmk zk /M
где М = Σm - масса тела. Масса точки или тела не зависит от действующих сил и, следовательно, центр масс существует даже тогда, когда отсутствуют силы тяжести. Таким образом, понятие центр масс более широкое, чем понятие центр тяжести. Если имеем тело, для которого силы притяжения можно считать параллельными и для всех точек тела ускорение g одинаково, то центр масс совпадает с центром тяжести.
Моментом инерции тела относительно какой-либо оси называют сумму произведений массы каждой точки тела на квадрат ее расстояния от этой оси:
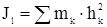
Единица измерения [J] = кг · м2
Если имеем сплошное твердое тело, то вместо конечной суммы в этой формуле будет определенный интеграл 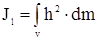 .
.
Для окружности или тонкой круглой цилиндрической оболочки Jl = MR2, где l - ось симметрии, перпендикулярная плоскости окружности или параллельная образующим цилиндра. Для круглого диска или однородного цилиндра Jl = ½ MR2. Для прямолинейного стержня длиной Jl =1/12Ma2, если ось l, перпендикулярная стержню, проходит через его середину, и Jl =1/3Ma2, если ось l перпендикулярная стержню, проходит через его конец.
1.5.2 Внешние и внутренние силы.
Механической системой, или просто системой, называют такое множество (конечное или бесконечное) материальных точек, и котором положение и движение любой точки зависит от положения и движения остальных точек системы. В динамике, помимо разделения сил на заданные и на реакции связей, принято также разделение сил на внешние и внутренние. Внешними силами для данной системы материальных точек называют силы, действующие на точки системы со стороны точек к системе не принадлежащих. Внутренними силами называют силы взаимодействия между точками системы. Внешние силы обозначим индексом (е), т.е. Fe, а внутренние - индексом (i), т.е. Fi.
Силы могут переходить из категории внешних в категорию внутренних и обратно в зависимости оттого, какие тела или точки объединяем в рассматриваемую систему. Согласно третьему закону Ньютона геометрическая сумма двух внутренних сил взаимодействия между каждыми двумя точками системы равна нулю, следовательно, геометрическая сумма всех внутренних сил системы равна нулю или, другими словами, главный вектор всех внутренних сил равен нулю:
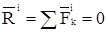
Можно также сделать заключение, что главный момент всех внутренних сил относительно произвольного центра О равен нулю:
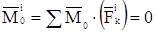
Дата добавления: 2015-08-08; просмотров: 944;
