В проекциях на оси координат
d(mvx)/dt = X ; d(mvy)/dt = Y ; d(mvz)/dt = Z.
Элементарным импульсом силы ds называют вектор, равный произведению вектора силы на элементарный промежуток времени:
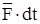 .
.
Из 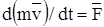 получаем другое выражение теоремы:
получаем другое выражение теоремы:
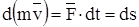 ,
,
т.е. дифференциал количества движения точки равен элементарному импульсу силы, действующей на эту точку.
Интеграл  называют полным импульсом силы за промежуток времени t – t0. Интегрируем последнее равенство в пределах от t0 до t, причем скорости в эти моменты времени обозначим через v0 и v:
называют полным импульсом силы за промежуток времени t – t0. Интегрируем последнее равенство в пределах от t0 до t, причем скорости в эти моменты времени обозначим через v0 и v:
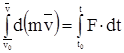 , но
, но 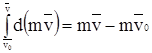 ,
,
тогда 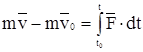 ,
,
Получили выражение теоремы об изменении количества движения точки в интегральном (конечном) виде: изменение количества движения точки за некоторый промежуток времени М равно полному импульсу силы, действующей на точку за тот же промежуток времени. Проектируя это равенство на оси координат, имеем
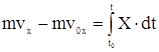
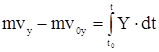
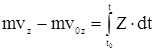
Рассмотрим систему материальных точек и применим формулу d(mv)/dt = F для k - ой точки системы:
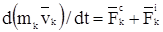 ,
,
где 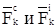 - равнодействующие внешних и внутренних сил, приложенных к k - ой точке. Суммируем эти равенства, написанные для всех точек системы и, принимая во внимание, что производная суммы функций равна сумме производных этих функций, получаем:
- равнодействующие внешних и внутренних сил, приложенных к k - ой точке. Суммируем эти равенства, написанные для всех точек системы и, принимая во внимание, что производная суммы функций равна сумме производных этих функций, получаем:
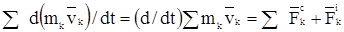 .
.
Т.к. 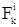 = 0, а
= 0, а 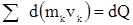 , то теорему об изменении количества движения системы можно представить в дифференциальном виде:
, то теорему об изменении количества движения системы можно представить в дифференциальном виде:
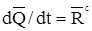 ,
,
где 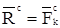 - главный вектор внешних сил. В проекциях на оси координат имеем:
- главный вектор внешних сил. В проекциях на оси координат имеем:
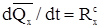 ,
, 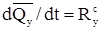 ,
, 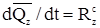
Из равенства 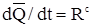 после умножения на dt и интегрирования в пределах от to до t получаем выражение теоремы в интегральном (конечном) виде:
после умножения на dt и интегрирования в пределах от to до t получаем выражение теоремы в интегральном (конечном) виде:
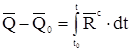 .
.
Изменение количества движения системы за некоторый промежуток времени t - tо равно полному импульсу главного вектора всех внешних сил, действующих на систему за тот же промежуток времени.
Проектируя последнее равенство на оси координат, получаем выражение теоремы в скалярной (координатной) форме:
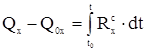 ,
, 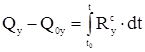 ,
, 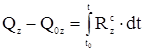
1.5.4 Теорема об изменении кинетической энергии системы.
Энергией называют способность тела совершать механическую работу. Кинетической энергией точки называют половину произведения массы точки на квадрат ее скорости: mv2/2. Единица измерения в системе СИ: [mv2/2] = кг м2 с2, а в технической системе единиц: [mv2/2] = кгс м. Кинетической энергией системы материальных точек называют сумму кинетических энергий всех точек системы:
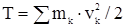
Рассмотрим частные случаи определения кинетической энергии твердого тела.
Поступательное движение твердого тела. Из кинематики известно, что скорости всех точек при поступательном движении тела равны между собой, и, следовательно, vk = vc, где vc - скорость центра масс. Тогда 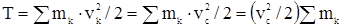 , но Σmk = M, где М - масса всего тела. Отсюда:
, но Σmk = M, где М - масса всего тела. Отсюда:  , т.е. кинетическая энергия поступательно движущегося твердого тела равна кинетической энергии центра масс, считая, что в нем сосредоточена масса всего тела.
, т.е. кинетическая энергия поступательно движущегося твердого тела равна кинетической энергии центра масс, считая, что в нем сосредоточена масса всего тела.
Вращение твердого тела вокруг неподвижной оси. При вращении тела vk = rk· ω, тогда: 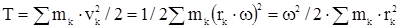 - момент инерции тела относительно оси вращения, тогда
- момент инерции тела относительно оси вращения, тогда
T = J · ω2/2,
т.е. при вращении твердого тела вокруг оси роль массы играет момент инерции.
Плоскопараллельное движение твердого тела. Пусть точка Р -мгновенный центр скоростей плоской фигуры. Тогда
T = J · ω2/2.
Обозначим через С центр масс плоской фигуры. По теореме о связи между моментами инерции относительно параллельных осей
Jp = Jc + (PC)2·M,
где М - масса тела; JP, JC - моменты инерции фигуры относительно осей, проходящих через точки Р и С перпендикулярно плоской фигуре. Находим
T = Jc · ω2/2 + (ω · PC)2 · M/2.
Скорость любой точки плоской фигуры равна произведению расстояния от точки до мгновенного центра скоростей на угловую скорость фигуры: Vc = PC · ω Получаем формулу
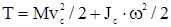 ,
,
где JC - момент инерции тела относительно оси, перпендикулярной к основной плоскости движения тела и проходящей через его центр масс - точку С.
Спроектируем вектор силы F = mа на касательную к траектории точки mat = Ft, где at = dv/dt. По определению проекции силы на ось: Ft = F· cosφ, где φ - угол между направлением силы и направлением элемента дуги (пути) ds. Получаем m(dv/dt) = F· cosφ. Умножим левую и правую части этого равенства на величину элемента пути ds, соответствующего промежутка времени dt, тогда m(dv/dt)·ds = F· cosφ·ds. Но v = ds/dt, и dA = F· cosφ·ds имеем m · v· dv = dA. Возьмем интегралы от обеих частей этого равенства:
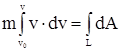
где L - обозначение дуги кривой, по которой перемещается точка.
Получаем выражение теоремы в интегральном (конечном) виде:
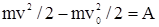
Итак, изменение кинетической энергии точки при некотором ее перемещении равно работе силы, действующей на эту точку на том же перемещении.
Считая v переменной величиной, продифференцируем поелелнее равенство но времени: d(m·v2/2)/dt=dA/dt.Умножая левую и правую части этого уравнения на dt, получим d(m·v2/2) = dA - т.е. дифференциал кинетической энергии точки равен элементарной работе силы, действующей на эту точку.
Для любой k-й точки системы материальных точек можно записать 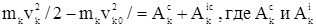 - работы внешних и внутренних сил, действующих на k-ю точку. Суммируя эти равенства, написанные для всех точек системы, имеем
- работы внешних и внутренних сил, действующих на k-ю точку. Суммируя эти равенства, написанные для всех точек системы, имеем 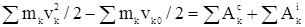 . Обозначим
. Обозначим 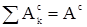 и
и 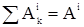 , где Ас и Аi - суммы работ внешних и внутренних сил системы при ее переходе из начального к конечному положениям. Учитывая, что
, где Ас и Аi - суммы работ внешних и внутренних сил системы при ее переходе из начального к конечному положениям. Учитывая, что 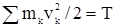 и
и 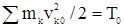 , получим выражение теоремы в интегральном (конечном) виде:
, получим выражение теоремы в интегральном (конечном) виде:
Т – Т0= Ас - Аi,
т.е. изменение кинетической энергии системы материальных точек при переходе системы из одного положения в другое равно сумме работ всех внешних и внутренних сил, действующих на систему при переходе между этими состояниями. Для абсолютно твердого тела сумма всех внутренних сил равна нулю: А'= 0, тогда Т – То = Ас.
1.5.5 Уравнение вращения тела вокруг неподвижной оси.
Для твердого тела, вращающегося вокруг неподвижной оси l, теорема об изменении кинетической энергии запишется в виде
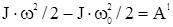
где J - момент инерции тел а относительно оси вращения.
Применим эту формулу для случая вращения твердого тела вокруг неподвижной оси с учетом того, что
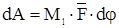
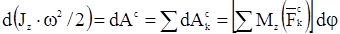
Получаем 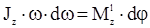 . Делим левую и правую часть этого равенства на dt, соответствующий углу dφ поворота тела
. Делим левую и правую часть этого равенства на dt, соответствующий углу dφ поворота тела 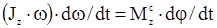 . Но
. Но 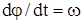 и
и 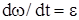 , тогда:
, тогда:
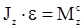
Произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающему моменту. При постоянном Мz, чем больше момент инерции тела, тем меньше угловое ускорение, т.е. Jz является мерой инертности тела при вращательном движении тела, как масса тела - при поступательном движении.
Учитывая, что г. 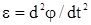 , получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси:
, получим дифференциальное уравнение вращения твердого тела вокруг неподвижной оси:
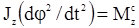 .
.
1.6 Основы теории механизмов и машин (ТММ).
1.6.1 Структурные элементы механизмов.
Механизмом называется совокупность подвижно соединенных звеньев тел, совершающих под действием приложенных к ним сил, определенные целесообразные движения. Машиной называется механизм или комплекс согласованно работающих механизмов, осуществляющих определенные целесообразные движения для преобразования энергии, материалов или информации.
В зависимости от выполняемых функций машины бывают:
1) энергетические (преобразующие энергию);
2) технологические, которые могут быть:
а) машины орудия - производящие работу;
б) транспортные - автомобили;
в) транспортирующие - конвейеры:
г) вычислительные.
В ТММ решаются две основные задачи:
1) исследование структурных, кинематических и динамических свойств существующих механизмов, т.е. анализ механизмов;
2) проектирование новых механизмов с заданными структурными, кинематическими и динамическими свойствами для осуществления требуемых движений, т.е. синтез механизмов.
Целью структурного и кинематического анализа механизмов является изучение их строения, исследование движения звеньев механизмов лишь с точки зрения геометрии независимо от сил, вызывающих движение этих тел. Цель динамического анализа - изучение методов определения сил, действующих на звенья механизма во время их движения, и исследование взаимосвязи между движениями звеньев и силами, на них действующими, в том числе (и прежде всего) массовыми силами (силами инерции). 11ель синтеза - проектирование механизма предварительно выбранной структуры по заданным кинематическим и динамическим свойствам.
|
|
|

|
Рис 18. Рис 19.
Рис 20. Рис 21.
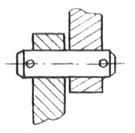
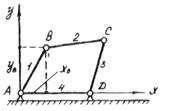
В ТММ вместо твердого тела введено понятие "звено". Звеном называется совокупность деталей машин, скрепленных друг с другом неподвижно. Деталью машины называют простейшую ее часть, изготовленную из однородного по марке материала без применения сборочных операций (шпонки, болт, зубчатое колесо). Всякий механизм машины состоит из отдельных звеньев, соединенных друг с другом, например, шарнирно (Рисунок 18).
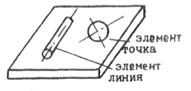
Соединение двух соприкасающихся звеньев, допускающее их относительное движение, называется кинематической парой (Рисунок 18). Поверхности, линии, точки соприкосновения звеньев называются элементами кинематической пары (Рисунок 19).
Связанная система звеньев, образующих между собой кинематические пары, называется кинематической цепью (Рисунок 20).
Звенья 1,2,3,4, соединенные шарнирами А, В, С, Д (кинематические пары) образуют кинематическую цепь. Элементы КП - поверхности. Кинематическая цепь хотя бы с одним неподвижным звеном образует механизм. Все неподвижные звенья образуют одну неподвижную систему тел - стойку (Рисунок 1.21).
Таким образом, в любом механизме мы имеем одно неподвижное звено и одно или несколько подвижных звеньев.
Например, закрепим неподвижно звено 4, получим кривошипно-коромысловый механизм (Рисунок 1.21 ). 3вено 1 - кривошип, звено, совершающее полный оборот вокруг оси. Звено 2 - шатун, звено, совершающее сложное плоскопараллельное движение. Звено 3- коромысло, звено, совершающее качательное движение. Звено 4 - стойка. Положение звеньев в любой момент времени можно выразить через координаты относительных осей, проведенных через центр вращения какого-либо звена, например, звена 1.
1.6.2 Кинематические пары и их классификация.
Если рассматривать звено, свободно движущееся в пространстве, то оно, как и любое твердое тело, обладает шестью степенями свободы Н = 6. Движение звена можно представить как поступательное и вращательное относительно произвольно выбранных координатных осей х, у, z (Рисунок 22).
Любая кинематическая пара (т.е. подвижное соединение 2-х звеньев) ограничивает те или иные относительные движения каждого звена.
Эти ограничения называют условиями связи -S. Очевидно, что число условий связи находится в пределах 1 < S< 5, т.к. при S = О звенья не соприкасаются и КП не существует; при S = 6, КП переходит в жесткое соединение 2-х звеньев. Тогда число степеней свободы - Н звена кинематической пары: Н = 6-S; и изменяется также в пределах 1 < Н < 5.
Под степенью свободы принято понимать простейшие движения, которыми может обладать точка или звено кинематической пары. Число условий связи S и число степеней свободы Н являются структурными характеристиками кинематических пар.
Классификация кинематических пар:
1) по количеству условий связи, наложенных на относительное движение звеньев кинематической пары, по предложению академика Артоболевского И.И. их делят на 5 классов (Таблица 1.1);
2) по виду элементов КП классифицируются на: высшие, у которых элементы точка, линия (I, II кл) и низшие – элементы поверхность (III, IV, V классы). Для того, чтобы элементы КП находились в постоянном соприкасании, они должны быть замкнуты. Низшие КП имеют геометрическое замыкание (IV, V). Для высших КП (I, II кл) замыкание должно быть силовое (вес, пружина).
3) по виду траектории кинематические пары классифицируются на: плоские - плоская траектория (IV, V) и пространственные - пространственная траектория (КП I,II,III класса).
1.6.3 Кинематические цепи и их классификация.
Кинематические цепи (КЦ) делятся на:
1) Простые и сложные.
Простые - если каждое звено входит не более, чем в 2 КП
(Рисунок 23. а, в).
Сложные - если хотя бы одно звено входит более, чем в 2 КП
(Рисунок .23. б).
2) Открытые (незамкнутые) и закрытые (замкнутые).
Дата добавления: 2015-08-08; просмотров: 1184;
