Внутренние силовые факторы.

Смещение атомов при деформациях материала под действием внешних сил сопровождается изменением так называемых внутренних сил взаимодействия между атомами. Эти внутренние силы сопротивляются стремлению внешних сил изменить форму и разрушить тело. Они стремятся восстановить первоначальную форму тела после снятия нагрузок т.е. освободить тело от упругих деформаций.

Внутренние межатомные силы, возникающие как результат деформации от внешних сил, и являются предметом изучения сопротивления материалов, так как именно их величина характеризует способность тел сопротивляться внешним воздействиям. Эти силы называют внутренними силовыми факторами (В.С.Ф.).

2.2.2 Формулы для расчета моментов инерции.

Момент инерции сложной фигуры относительно какой-то оси равен сумме моментов инерции простых элементов этой фигуры относительно той же оси.

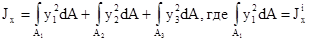и т.д.

Сумма осевых моментов инерции относительно перпендикулярных осей есть величина постоянная и равна полярному моменту инерции относительно точки пересечения этих осей:

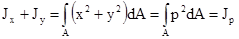
Момент инерции фигуры относительно оси параллельной центральной оси равен центральному моменту инерции плюс произведение площади на квадрат расстояния между осями:

y = y_c +a; x = x_c + b

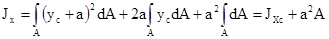
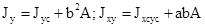
Моменты инерции относительно осей х_α и у_α , повернутых на угол α относительно исходных осей х и у:

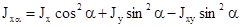
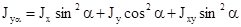
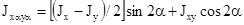
Очевидно, что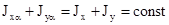

Таким образом, моменты инерции являются непрерывными функциями угла α. Возможно, такое положение осей координат, при котором J_xαyα=0

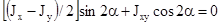
откуда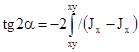

Оси, относительно которых центробежный момент инерции равен нулю, называют главными осями инерции. Осевые моменты инерции относительно главных осей имеют наибольшее и наименьшее значение из всех возможных

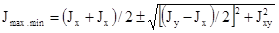
2.2.3 Моменты сопротивления.

Осевым моментом сопротивления сечения называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки от этой оси:

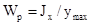
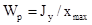
Полярный момент сопротивления сечения - это отношение полярного момента инерции сечения к расстоянию от центра до наиболее удаленной точки:

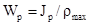
Моменты сопротивления характеризуют сопротивление сечения кручению и изгибу. Поэтому их необходимо знать при инженерных расчетах на прочность. Моменты сопротивления измеряют в единицах длины в третьей степени, мм³, м³.

2.2.4 Моменты инерции и моменты сопротивления простых фигур.

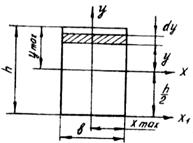
Определим моменты инерции прямоугольника высотой h и шириной b (Рисунок 42).

Момент инерции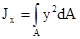

Выделим в прямоугольникe элементарную полоску высотой dy и шириной b. Элементарная площадь dA = bdy.

При этом у изменяется от - h/2 до + h/2, тогда

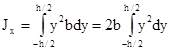
Рис 42.

Откуда 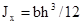; аналогично .

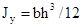Момент инерции относительно оси х₁, проходящей через основание

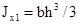
Моменты сопротивления

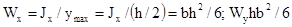
Круглое сечение диаметром - d (Рисунок 43. а).

Для круглого сечения ;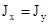

; ;

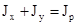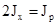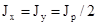
Полярный момент инерции .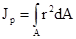

Выделим элементарное кольцо толщиной dρ на текущем радиусе – ρ. Площадь элементарного кольца dA=2π·ρ·dρ.

Тогда 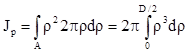, т.е

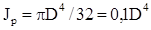
Осевые моменты инерции: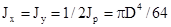

Полярный момент сопротивления:

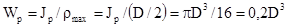
Рис 43.

Осевые моменты сопротивления:

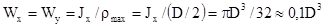
Кольцевое сечение с наружным D и внутренними диаметрами (Рисунок 43. б).

Полярные и осевые моменты инерции могут быть получены как разность, соответственно полярных и осевых моментов инерции большого и малого круга

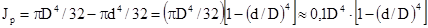
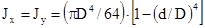
Моменты сопротивления:

Полярный .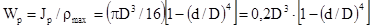

Осевые .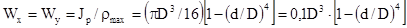

Моменты инерции и моменты сопротивления прокатных профифилей приводятся в таблицах справочников сортамента (Рисунок 44).

Рис 44.