Сложное движение точки

Систему координатных осей O_XYZ выбираем за основную, условно неподвижную, а систему осей O_X1Y1Z1 считаем подвижной (Рисунок 16). Необходимо помнить, что движение одной и той же точки М или тела по отношению к этим двум системам отсчета происходит по-разному.

Движение точки или тела, относительно неподвижной системы координат называют абсолютным движением, а движение относительно подвижной системы координат - относительным движением. Абсолютное и относительное движения точки можно связать с помощью понятия переносного движения. Следует помнить, что движение рассматриваемой точки не связано с движением подвижной системы координат (ее выбор зависит от нас), но можно представить себе, что точка внезапно в данный момент стала одним целым с подвижными осями и начала двигаться вместе (слитно) с ними. Некоторая область пространства вокруг подвижных осей как бы внезапно замерзла, захватив вместе с этими осями также и точку М. Воображаемое движение точки в данный момент вместе, как одно целое с подвижными осями относительно неподвижных осей называют переносным движением точки для данного момента времени.

Скорость и ускорение точки по отношению к подвижной системе координат называют относительными, по отношению к неподвижной -абсолютными, а вместе (слитно) с подвижными осями относительно неподвижных осей - переносными. Абсолютное движение точки, или тела, для каждого данного момента времени складывается из переносного и относительного движений этой точки, или тела.

Абсолютная скорость точки равна векторной сумме ее переносной и относительной скоростей:

Если подвижные оси координат перемешаются поступательно, то абсолютное ускорение точки равно геометрической сумме ее переносного и относительного ускорений:

Если подвижные оси координат перемешаются не поступательно, то в правой части этого уравнения нужно прибавить так называемое кориолисово ускорение.

1.4 Динамика, дифференциальные уравнения движения точки, принцип Даламбера

Основные понятия и аксиомы динамики

Динамика является разделом теоретической механики, в котором изучается движение материальных точек и тел под действием приложенных к ним сил.

Аксиома 1 - закон инерции, рассмотренный ранее в разделе "Статика": всякая изолированная материальная точка находится в равновесии, пока какая-нибудь причина не выведет ее из этого состояния.

Аксиома 2 - основной закон динамики: сила, действующая на материальную точку, прямо пропорциональна вызываемому ее ускорению и направлена по вектору ускорения. Коэффициент пропорциональности т называют массой точки:

F = ma; или

Каждая материальная точка, или тело, имеет свой, строго определенный коэффициент пропорциональности - массу точки. Масса материальной точки - физическая величина, характеризующая инертные и гравитационные свойства точки и являющаяся мерой этих свойств. Для свободного падения в пустоте F = G, где G - сила тяжести; a = g, g = 9,81 м/с²- ускорение свободного падения, одинаковое для всех тел. При этом масса: m = G/g.

Из закона F = m · a берут начало две принципиально отличные системы единиц: физическая и техническая. В физической системе единиц за основные принимаются единицы длины, времени и массы. Международная система единиц (СИ) является физической системой, в которой приняты единицы: 1 м, 1 с и 1 кг м массы. Размерность единицы силы в этой системе: [F] = [m][a]= кг · м/с². Полагая m = 1 кг; а = 1 м/с², получим силу, называемую Ньютоном: F = 1 Н. Итак, Ньютон - это сила, сообщающая массе в 1 кг ускорение, равное 1 м/с².

В технической системе единиц за основные принимаются единицы длины, времени и силы (кгс).

Связь между системами единиц основана на том, что масса в 1 кг притягивается к Земле 1 кгс (сила).

Сила тяжести G = mg = 1 кг · 9,81 кг · м · с² = 9,81 Н.

Итак, 1 кгс = 9,81 Н; 1 Н = 0,102 кгс

Аксиома 3.Две материальные точки действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны по прямой, соединяющей эти точки.

Аксиома 4. (принцип независимости действия сил). Ускорение, получаемое материальной точкой при одновременном действии на нее нескольких сил, равно векторной сумме ускорений, которые сообщила бы каждая сила, действуя отдельно:

,

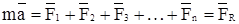где 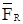- равнодействующая системы сил.