Проекция на ось силы и векторной суммы сил.
Осью называют бесконечную прямую, для которой одно из двух направлений вдоль прямой выбрано как положительное. Проекцией силы на ось является прямолинейный отрезок, ограниченный перпендикулярами, опущенными из начала и конца вектора силы на данную ось. Если направление от начала проекции А к концу проекции С совпадает с положительным направлением оси, то величину проекции берут со знаком плюс, а в противоположном случае - со знаком минус. При определении проекции силы па ось можно силу или ось переносить параллельно так, чтобы получились пересекающиеся прямые и силу считать приложенной в какой либо точке оси.
При определении проекции силы умножают модуль силы на косинус се острого угла с осью (Fcosb). Если сила параллельна оси, то ее проекция на ось равна модулю силы со знаком плюс или минус в зависимости от того, совпадает или нет направление силы с положительным направлением оси. Если сила перпендикулярна оси, то ее проекция на эту ось равна нулю.
Правило силового треугольника: Равнодействующая двух сил имеет начало в начале первой силы и конец - в конце второй силы (Рисунок 5).
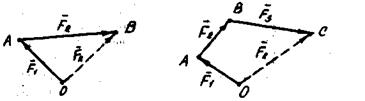
Рис 5.
Чтобы сложить систему сил. приложенных в одной точке, надо от конца первой силы отложить вектор второй силы, а от конца второй силы отложить вектор третьей силы и т.д. Вектор равнодействующей Рк.
имеет начало в начале первой силы и конец - в конце последней силы, т.е. равнодействующая равна векторной сумме всех заданных сил:
FR = F1 + F2 + F3 +…Fn = SFk
Векторная сумма сил, направленных в одну сторону но одной прямой, направлена в ту же сторону и равна по модулю арифметической сумме модулей составляющих сил. а если силы направлены но прямой в противоположные стороны, то модуль равнодсйствующей равен абсолютному значению алгебраической суммы величин составляющих сил. причем равнодействующая направлена в сторону большей по модулю силы (Рисунок 6).
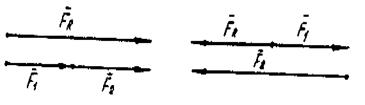
|
Рис 6.
Проекция векторной суммы сил на какую-либо ось равна сумме-проекции составляющих сил на ту же ось:
|
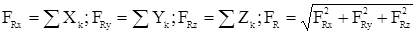 . Равнодействующая
. Равнодействующая 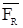 трех сил
трех сил 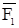 ,
, 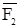 ,
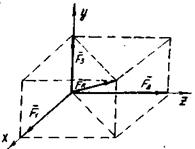
, 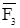 , приложенных в одной точке, приложена в той же точке и равна по величине и направлению диагонали параллелепипеда, ребра которого равны и параллельны заданным силам (Рисунок 7).
, приложенных в одной точке, приложена в той же точке и равна по величине и направлению диагонали параллелепипеда, ребра которого равны и параллельны заданным силам (Рисунок 7).
Согласно этому правилу заданную силу Рк можно разложить по трем заданным осям (направлениям) к, у, 1 единственным образом:
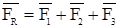 .
.
|
Дата добавления: 2015-08-08; просмотров: 1675;
