Движение электрона в однородном электрическом поле

Электроды плоскопараллельны на расстоянии d один от другого (рис. 3.1).

Уравнение Лапласа, имеющее вид 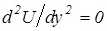, после интегрирования сводится к уравнению

.

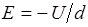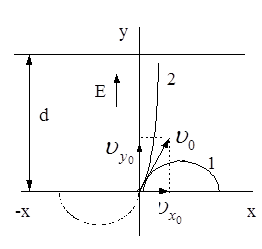
Рис. 3.1 – Движение электрона в однородном электрическом поле

Уравнение движения электрона в прямоугольной системе координат разбивается на три уравнения:

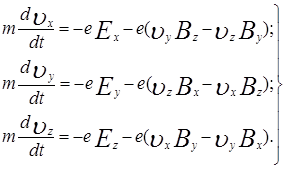
В рассматриваемом случае магнитное поле отсутствует, а электрическое имеет одну компоненту 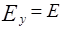. Тогда система уравнений запишется как

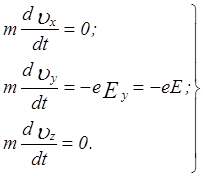
Пусть в момент 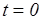электрон находится в точке начала координат и движется со скоростью « 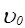«, имеющей компоненты по осям х и y, а компонента скорости по z равна нулю. Тогда интегрирование приводит к уравнениям:

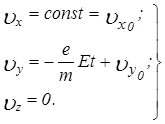
После повторного интегрирования первых двух уравнений получаем

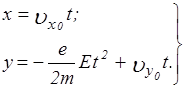
Константы интегрирования в обоих случаях равны нулю, поскольку в начальный момент 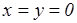интегрирование третьего уравнения дает .

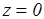Исключим :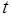

.

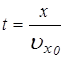Получим уравнение траектории электрона:

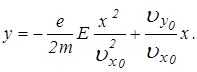
Видно, что движение происходит по параболе (кривая 1 на рис. 3.1), обращенной выпуклостью вверх. Анализ показывает, что вершина этой параболы имеет координаты 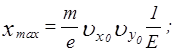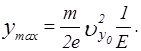Совершая движение по этой траектории, электрон возвращается к оси х в точке с координатой:

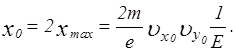
Если вектор напряженности поля 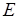направить в противоположную сторону 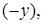то изменяется знак первого члена уравнения траектории электрона:

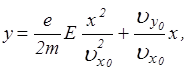
т.е. в данном случае электрон будет двигаться по траектории 2 (на рис. 3.1). Это отрезок параболы, симметричный относительно начала координат параболе 1.