Движение электронов в вакууме в электрическом и магнитных полях

В электрическом поле напряженностью Е на электрон действует сила 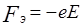, противоположная по направлению вектору Е.

В магнитном поле с индукцией В на движущийся электрон действует сила Лоренца. При произвольной ориентации векторов эту силу удобно представить в векторной форме:

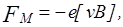
где 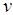– вектор скорости электрона.

При наличии электрического и магнитного полей действующая на электрон сила:

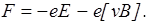
Поскольку при движении в вакууме электрон не испытывает столкновений, приводящих к изменению величины и направления его скорости, получаем уравнение движения электрона

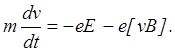
Это уравнение позволяет полностью описать движение электрона, найти его траекторию и скорость в любой точке, если известны начальные условия: координаты, величина и направление скорости в начале пути и, главное, если известна картина поля, т.е. заданы в виде функции координат векторы напряженности электрического поля 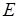и магнитной индукции .

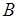Нахождение картины поля является первым этапом решения задач о движении электронов в межэлектродном пространстве.

Аналитически картину электрического поля в пространстве, свободном от зарядов, можно найти решением уравнения Лапласа:

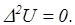
Это для случая малых потоков или единичных электронов.

В случаях, когда электроны и другие заряженные частицы находятся в межэлектродном пространстве в большом количестве и влияют на картину электрического поля, в основу расчета должно быть положено уравнение Пуассона:

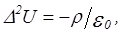
где 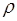– плотность объемного заряда;

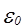– диэлектрическая проницаемость.

Однако картины электрического поля аналитическим путем можно найти для простых конфигураций электродов, а для сложных электродов используют эксперимент (электрическая ванна, метод сеток, метод сопротивлений) или приближенные методы расчета.

Картину магнитного поля также можно получить аналитически только для простейших случаев.

Вернемся к уравнению:

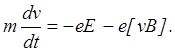
Умножив левую и правую части скалярно на скорость электрона 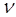, получим

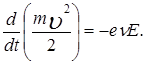
Второе слагаемое равено нулю потому, что сила Лоренца перпендикулярна направлению движения электрона.

Выясняется, что под действием магнитного поля изменяется только направление движения электрона, а его скорость не меняется по величине.

Электрическое поле влияет на кинетическую энергию и на направление движения.

Уравнение, связывающее энергию свободного электрона с пройденной разностью потенциалов U:

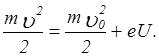
Если начальную энергию электрона охарактеризовать некоторой разностью потенциалов U₀ , т.е. выразить ее в электрон-вольтах, то скорость электрона, прошедшего разность потенциалов U,

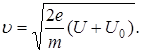
Напомним, что при скоростях электрона, близких к скорости света, во всех приведенных уравнениях должна быть релятивистская масса электрона. Однако, как показывает расчет, релятивистский эффект учитывается только при анализе движения электрона, ускоряемого разностью потенциалов в несколько десятков киловольт. Поэтому далее будем считать массу электрона постоянной.