ГАРМОНИЧЕСКИЙ КВАНТОВЫЙ ОСЦИЛЛЯТОР

Гармонический осциллятор – одна из моделей, наиболее часто используемых в различных разделах физики. Эта модель описывает, например, малые колебания атомов вблизи положений равновесия в кристаллах, стоячие электромагнитные волны в полости и, поэтому, играет важную роль в теории колебательных спектров молекул, при изучении теплоемкости твердых тел, для объяснения механизма дисперсии и т.д.

Под линейным гармоническим осциллятором понимается частица массой m, совершающая гармонические колебания с частотой w_о и амплитудой х_m под действием гармонической (квазиупругой) силы.

Потенциальная энергия W_p такой частицы будет иметь вид параболической потенциальной ямы (рис.2.11), поскольку

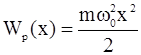. (2.56)

В классической физике энергия W такой частицы может принимать любое значение, в том числе и равное нулю. Кроме того, за пределы области 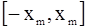классический осциллятор выйти не может.

Рис.2.11

В квантовой механике наличие граничных условий при больших смещениях |х| частицы от положения равновесия приводит к тому, что разрешенным будет лишь набор энергий W_n : энергетический спектр квантового гармонического осциллятора будет дискретным.

В справедливости этого можно убедиться, решив уравнение Шредингера для осциллятора с учетом (2.56):

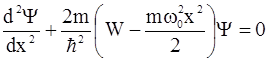. (2.57)

Его частное решение будем искать в виде функции Гаусса

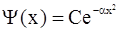, (2.58)

где С – некоторая константа.

Подставив (2.58) в (2.59), получим

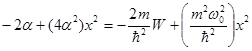. (2.59)

Приравнивая коэффициенты при х², имеем

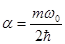. (2.60)

Из сравнения свободных слагаемых в (2.59) вытекает

.

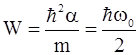Таким образом, функция (2.58) является решением уравнения (2.57) лишь при условии, что энергия осциллятора равна

. (2.61)

В этом случае, с учетом соотношения (2.60), получим Y - функцию (2.58) в виде

.

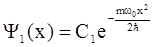Путем подстановки можно убедиться, что при условии W₂ 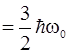решением уравнения (2.57) будет функция

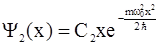. (2.62)

Следует заметить, что разность (W₂ –W₁), то есть расстояние между соседними энергетическими уровнями квантового осциллятора, равна:

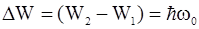
Это справедливо и для более высоких энергетических уровней, описываемых общей формулой:

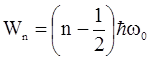, (2.63)

где n = 1,2,3, ….. , ¥ -главное квантовое число.

При n = 1, W_n = W₁ (формула (2.61)),

при n = 2, W_n = W₂ (формула (2.62)).

Таким образом, энегрия квантового осциллятора квантуется. Кроме того, она в принципе не может обращаться в нуль: минимальная энергия – энегрия нулевых колебаний осциллятора - равна W_min=W₁= 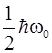(см.рис.2.12).

Значит, частица не может находиться на дне потенциальной ямы. Этот вывод следует из соотношения неопределенностей Гейзенберга (см. § 2.3.2 ).

Действительно, “падение” на дно ямы связано с обращением в нуль импульса частицы, что означает обращение в нуль неопределенности DP_x импульса. Тогда, в соответствии с соотношением неопределенностей, становится сколь угодно большой неопределенность Dx координаты, что в свою очередь, противоречит пребыванию частицы в потенциальной яме.

Возбуждение добавляет к энергии основного состояния величину целую кратную 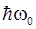, т.е. 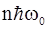, как постулировал Планк в теории излучения абсолютно черного тела (см.п 1.7).

Строгое решение задачи о квантовом осцилляторе показывает, что частицу можно обнаружить и за пределами дозволенной области |х| 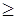х_m, поскольку существует отличная от нуля вероятность нахождения частицы в этой области. На рис.2.13 сопоставляются квантовая и классическая плотности вероятностей 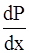обнаружения частицы в области от х до (х+dх) при n =2.

Рис.2.12 Рис.2.13