Механические гармонические колебания. Гармонический осциллятор

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени.

Колебательную систему вне зависимости от ее физической природы называют осциллятором(груз, подвешенный на нти).

Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и др. Однако различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями.

Колебания условно делят на простые и сложные. К ним относятся: свободные колебания, затухающие колебания и вынужденные колебания.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на тело или систему.

Гармонические колебания – колебания, при которых колеблющаяся физическая величина изменяется во времени по закону синуса (косинуса).

Гармонические колебания описываются уравнением

x = A sin (ω_ot + φ_o),(1)

где х –смещение;

А – амплитуда;

(ω_ot+φ_o) – фаза колебаний;

φ_o – начальная фаза.

Первая производная от смещения по времени определит выражение для скорости колеблющейся точки:

. (2)

Cкорость достигает максимального значения в момент времени, когда cos (ω_ot + φ_o) = 1, тогда .

Для определения ускорения колеблющейся точки найдем вторую производную от смещения по времени:

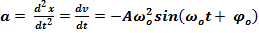. (3)

Максимальное ускорение - .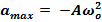

На рис.1. представлены графические зависимости смещения, скорости и ускорения. Из рисунка видно, что скорость достигает максимального значения, когда колеблющаяся точка проходит положение равновесия. В этот момент смещение и ускорение равны нулю.

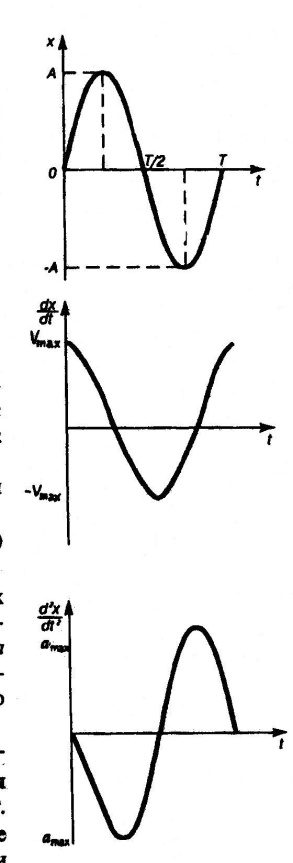
Рис.1