Свободные гармонические колебания в колебательном контуре

Колебательный LC контур - это электрическая цепь состоящая из индуктивности и емкости (рис.2а,б,в,г,д).

Рис. 2

В рассматриваемой электрической цепи могут происходить периодические изменения заряда q, напряжения u (или разности потенциалов) на обкладках конденсатора и электрического тока i.

Если емкость С поместить заряд q₀, то конденсатор заряжается, получая энергию 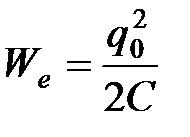. Разность потенциалов на обкладках конденсатора будет иметь максимальное значение U_c, а тока в цепи контура LC не будет (рис.2а).

При замыкании конденсатора на катушку индуктивности происходит разряд конденсатора. В результате разряда конденсатора на катушку индуктивности в ней появляется ток и, вследствие явления самоиндукции, электрический ток в цепи будет постепенно увеличиваться и достигнет максимального значения i₀ в момент времени 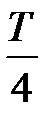, когда заряд q и напряжение u равны нулю (рис.2б). Далее ток в цепи, сохраняя прежнее направление, будет постепенно уменьшаться и станет равным нулю в момент времени . При этом заряд конденсатора и разность потенциалов между его обкладками вновь достигнут максимального значения (рис.2в), но в этот момент времени знаки зарядов пластин и направление напряженности электрического поля между обкладками конденсатора будут противоположны тем, что были в начальный момент времени.

В результате, вследствие явления самоиндукции, происходит перезарядка конденсатора. В следующие критические промежутки времени от до 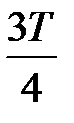и далее до Т процессы происходят в обратном направлении (рис.2г,д).

Для получения уравнения электромагнитных колебаний в рассматриваемом LC контуре используется закон Ома, согласно которому алгебраическая сумма падений напряжений равна алгебраической сумме действующих в этой замкнутой электрической цепи электродвижущих сил. В рассматриваемой электрической цепи LC действует только ЭДС самоиндукции 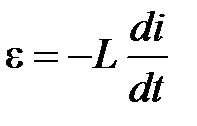, а падение напряжения происходит только на конденсаторе, поэтому 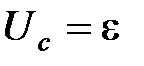. Но, по определению, 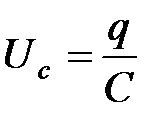, тогда

.

Принимая во внимание, что 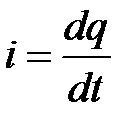и 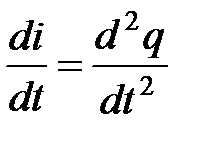получим:

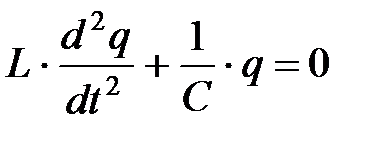или .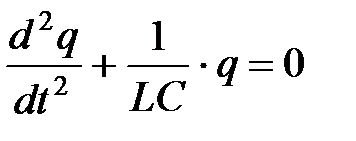

Введя обозначение 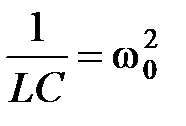, (4)

получается дифференциальное уравнение для электрической LC цепи:

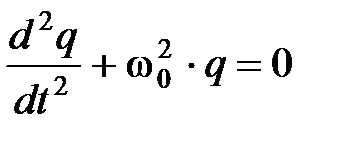. (5)

Решением данного дифференциального уравнения второй степени будет

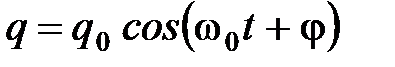. (6)

Следовательно, законы изменения тока и напряжения в цепи LC будут:

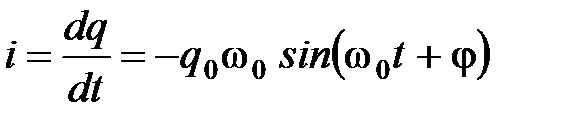, (7)

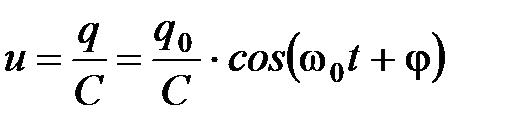. (8)

Графическое изображение изменения заряда, тока и напряжения в контуре представлены на рис.3.

Рис.3

При изменении величины заряда и тока будут изменяться напряженности электрического и магнитного полей. С увеличением заряда будет увеличиваться энергия электрического поля 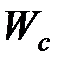конденсатора, а с увеличением тока будет увеличиваться энергия магнитного поля катушки индуктивности 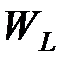. Энергия электрического поля будет переходить в энергию магнитного поля и обратно. Поэтому процессы, происходящие в колебательном контуре, носят название электромагнитных колебаний.

Тема 9. Затухающие и вынужденные колебания.

Вопросы:

1. Затухающие колебания.

2. Вынужденные колебания.

1. Затухающие колебания.