Упругие волны. Кинематика и динамика волновых процессов.

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной).

При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Среди разнообразных волн встречающихся в природе и технике выделяются следующие их типы:

волны на поверхности жидкости;

упругие волны;

электромагнитные волны.

Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные.

Для характеристики волн используется:

Длина волны это расстояние, которое проходит волна за время одного периода (рис.1).

, (1)

ξ λ   В О х х

Рис.1

Волновое число

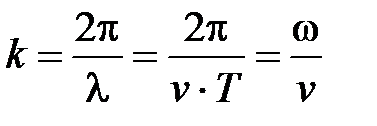. (2)

Бегущими волнами называются волны, которые переносят в пространстве энергию.

Перенос энергии волнами количественно характеризуется вектором плотности потока энергии.

Этот вектор для упругих волн называется вектором Умова (русский ученый, 1846-1915), решившего задачу о распространении энергии в среде. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.

Колебания точек описываются функцией

,

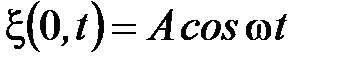для прохождения волной расстояния х требуется время 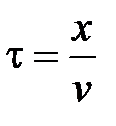, где v – скорость распространения волны.

Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид

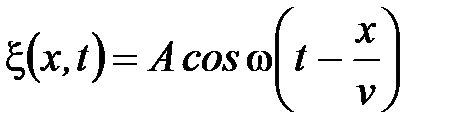, (3)

откуда следует, что ξ = ξ(х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (3) есть уравнение бегущей волны.

Если плоская волна распространяется в противоположном направлении, то

.

В общем случае уравнение плоской монохроматической бегущей волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

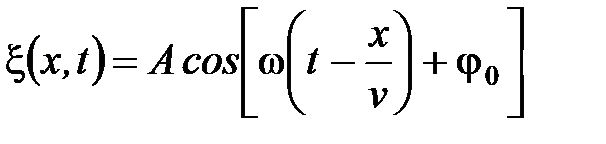, (4)

где А – амплитуда волны, ω – циклическая частота, φ₀ – начальная фаза волны, определяемая в общем случае выбором начал отсчета х и t, 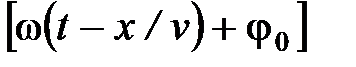- фаза плоской волны.

Учитывая волновое число уравнение (4) можно переписать в виде

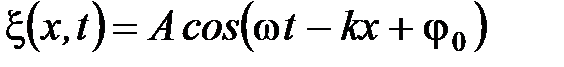. (5)

Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (5) только знаком члена kx.

Основываясь на формуле Эйлера, уравнение плоской волны можно записать в виде

,

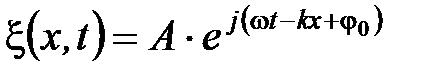где физический смысл имеет лишь действительная часть.

Предположим, что при волновом процессе фаза постоянна, т.е.

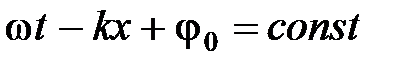. (6)

Продифференцировав (6) и сократив на ω, получим 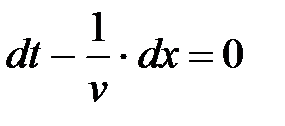, откуда

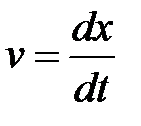. (7)

Следовательно, скорость распространения волны v в (7) есть не что иное, как скорость перемещения фазы волны, ее называют фазовой скоростью.

Повторяя ход рассуждений для плоской волны, можно доказать, что уравнение сферической волны – волны, волновые поверхности которой имеют вид концентрических сфер, записываются как

. (8)

где r – расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 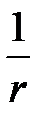. Уравнение (8) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным).

Из выражения (4) следует, что фазовая скорость

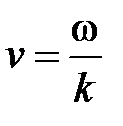. (9)

Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется дисперсионной средой.