Вынужденные колебания. Для получения незатухающих колебаний в системе (механической, электрической, электромеханической, электронной и др.) к ней необходимо подводить энергию для

Для получения незатухающих колебаний в системе (механической, электрической, электромеханической, электронной и др.) к ней необходимо подводить энергию для компенсации внутренних потерь. Компенсировать потери энергии можно с помощью внешнего воздействия, которое в общем случае может быть постоянной или изменяться со временем по какому – то закону. Под действием постоянного внешнего воздействия колебания в системе прекратятся, и движение механической системы будет поступательным. Под действием периодически изменяющегося внешнего воздействия в рассматриваемой системе будут происходить колебания, которые теперь уже будут не свободными, а вынужденными.

Вынужденными называются колебания, которые возникают в системе под действием внешнего периодически изменяющегося воздействия. Характер вынужденных колебаний (величины: амплитуда, частота) будет в этом случае определяться характером внешнего возмущающего воздействия и свойствами (характеристиками) самой системы в целом или характеристиками ее отдельных узлов и элементов.

При внешнем возбуждении системы ее сводные колебания в значительной мере будут определять ее вынужденные колебания и резонансные свойства.

Понятие вынужденных колебаний может быть приближенно распространено на системы, содержащие консервативные и нелинейные элементы, если их воздействие приводит к резким (или скачкообразным) изменениям амплитуд и фаз свободных (нормальных колебаний).

Так как свободные колебания в самой системе являются затухающими, то через определенный промежуток времени (времени переходного процесса или процессов) они прекратятся, и в системе установятся вынужденные колебания с частотой внешнего воздействия.

Графическое изображение переходного процесса показано на рис.4а.

Рис.4

В качестве примера вынужденных колебаний рассмотрим замкнутую электрическую цепь (рис.4б) состоящую из последовательно соединенных: емкости C, индуктивности L и активного сопротивления R, к которым подключен внешний источник энергии с ЭДС изменяющийся по гармоническому закону:

,

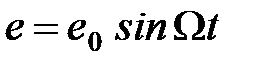где Ω – частота внешней вынуждающей ЭДС.

В рассматриваемом замкнутом электрическом контуре сумма падений напряжений на различных участках равна сумме действующих в нем ЭДС, поэтому

.

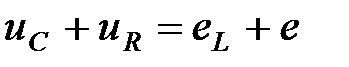Принимая во внимание соотношения 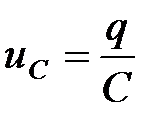, 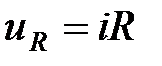и получим новый вид уравнения суммы падений напряжений и ЭДС в электрической цепи

,

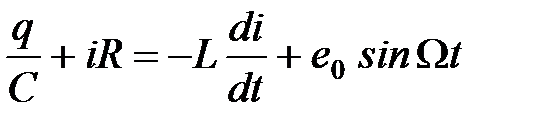или

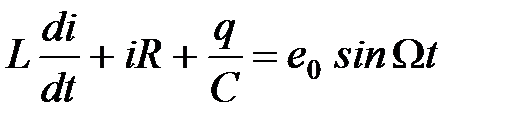. (3)

Дифференцируя по времени последнее уравнение (1) и учитывая 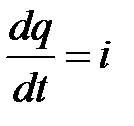получим уравнение

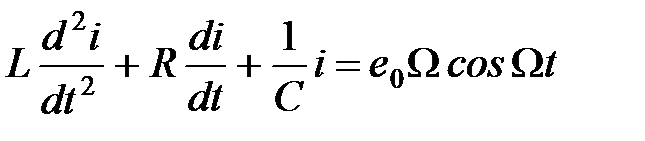. (4)

Решение дифференциального уравнения (4) имеет вид:

, (5)

где 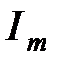- значение амплитуды установившегося тока в замкнутом электрическом контуре; φ – начальная фаза вынужденных колебаний. Требуется определить аналитические выражения 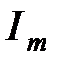и φ в соответствии параметрами рассматриваемого электрического контура и характеристик внешней возмущающей ЭДС.

Возьмем первую и вторую производные от выражения (5) и подставим из в формулу (4). После сокращения правой и левой частей уравнения на Ω получим:

.

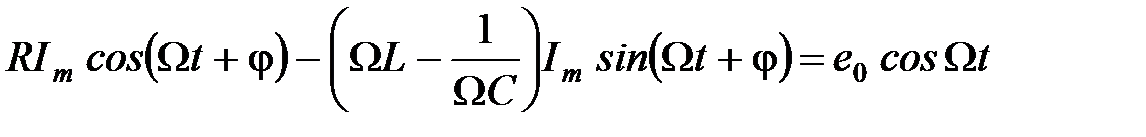Используя тригонометрические формулы для дальнейших преобразований и перенося все члены в левую часть получим:

.

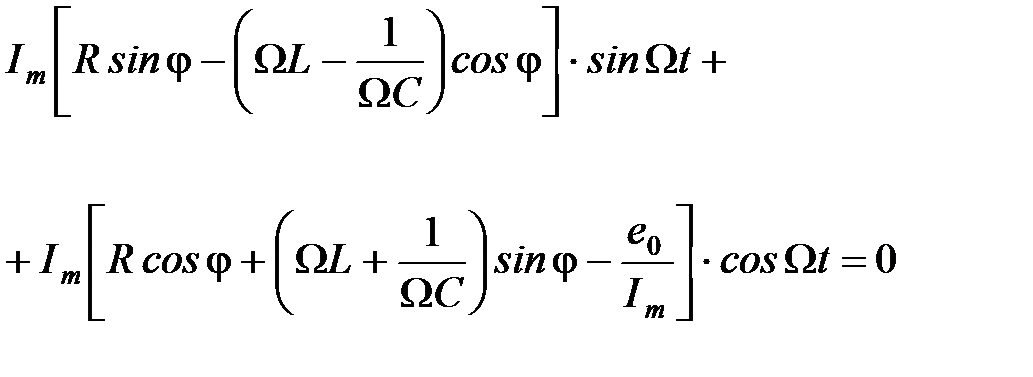Последнее равенство должно выполняться для любого момента времени, поэтому коэффициенты пр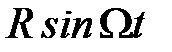и и 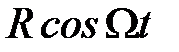должны равняться нулю, т.е.

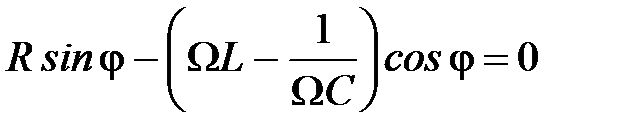; (6)

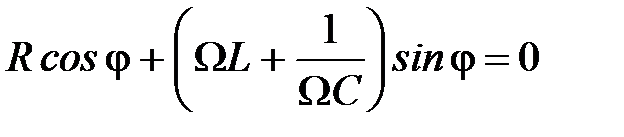. (7)

Из уравнения (6) следует:

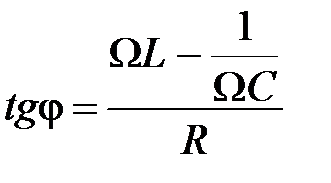. (8)

Возведя в квадрат равенства (6) и (5), а затем суммируя полученные выражения, получим:

,

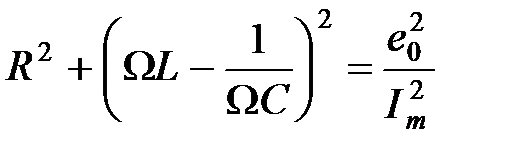откуда следует 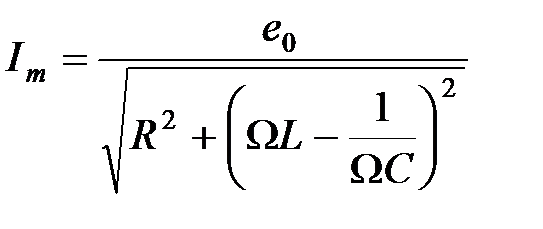. (9)

Полное сопротивление рассматриваемой электрической цепи (модуль комплексного сопротивления цепи) будет определяться выражением:

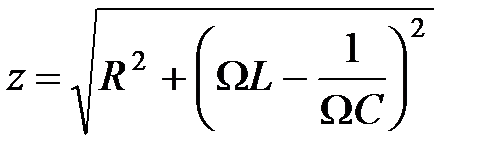, (10)

где 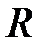- активное сопротивление цепи, 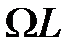- индуктивное сопротивление цепи, 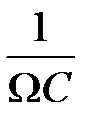- емкостное сопротивление рассматриваемой электрической цепи.

Примерами вынужденных колебаний могут служить колебания механической конструкции под действием переменной нагрузки; колебания мембраны датчика под действием переменного магнитного поля; колебания тока и напряжения в электрической цепи под действием переменной ЭДС и др.

Резонанс может возникнуть лишь в том случае, когда частота гармонических внешних воздействий близка к одной из собственных частот системы либо к их линейной комбинации, если внешнее воздействие меняет параметры системы (параметрический резонанс). При этом важным оказывается также и пространственное распределение воздействия – максимальный эффект достигается при соблюдении не только временного, но и пространственного синхронизма (нелинейная оптика).

Рассмотрим и математически опишем явление резонанса на примере электрической цепи (рис.4б). Если индуктивное сопротивление оказывается равным емкостному сопротивлению, т.е. 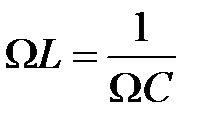, (11)

то полное сопротивление электрической цепи уменьшится (как будто в электрической цепи имеется только активное R сопротивление). В результате будет наблюдаться значительный рост амплитуды тока 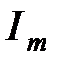циркулирующего в рассматриваемой цепи.

Из равенства (11) следует, что произойдет данный эффект при частоте вынужденных колебаний, равной .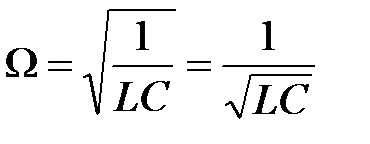

Однако, из ранее проведенного анализа данного контура следует, что 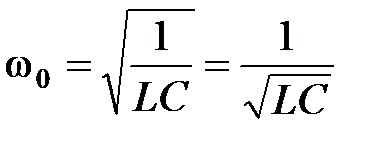- есть частота собственных колебаний контура.

Поэтому, явление резкого возрастания амплитуды установившихся вынужденных колебаний, проявляющееся при приближении значения частоты внешнего возмущения Ω к частоте собственных колебаний системы ω₀, называется резонансом.

В колебательном RLC контуре величина тока при резонансе будет тем больше, чем меньше будет омическое сопротивление рассматриваемой электрической цепи (рис.2).

Рис.2

Количественной характеристикой резонансных свойств колебательной системы принято считать ее добротность. Она показывает, во сколько раз амплитуда установившихся вынужденных колебаний превышает амплитуду вынужденных колебаний вдали от резонанса, т.е. в той области частот, где амплитуда вынужденных колебаний не зависит от частоты.