Теорема Гаусса для поля B
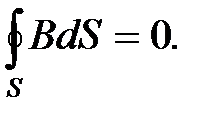
Итак, полная система уравнений Максвелла в интегральной форме:
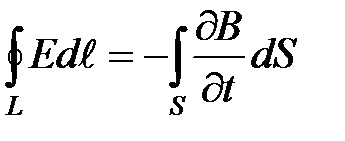
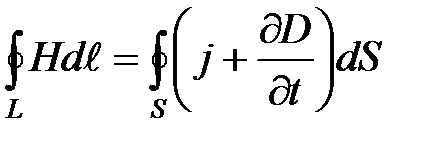
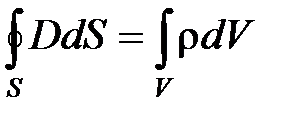
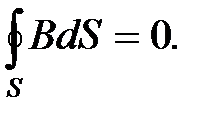
Интегральные и дифференциальные уравнения Максвелла не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной Среды. Их необходимо дополнить соотношениями, связывающими векторы Е, Н, D , B и j, которые не являются независимыми. Связь между ними определяется свойствами среды и ее состоянием, причем D и j выражаются через Е, а В через Н:
D=D(E), B=B(H), j=j(E).
Эти уравнения называются уравнениями состояния или материальными уравнениями, они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определенную форму.
В вакууме D = E и B = H. Совокупность уравнений поля и уравнений состояния образуют полную систему уравнений.
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь:
D = 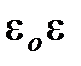 E, В =
E, В = 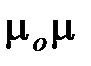 Н, j=
Н, j= 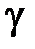 E.
E.
где 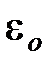 и
и 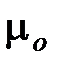 — соответственно электрическая и магнитная постоянные,
— соответственно электрическая и магнитная постоянные,
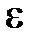 и
и 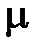 — соответственно диэлектрическая и магнитная проницаемости,
— соответственно диэлектрическая и магнитная проницаемости,
 — удельная проводимость вещества.
— удельная проводимость вещества.
Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями. Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.
Для стационарных полей (Е=const и В=const) уравнения Максвеллапримут вид
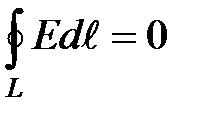
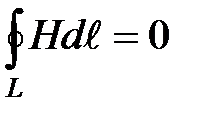
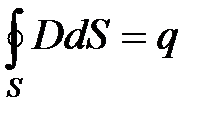
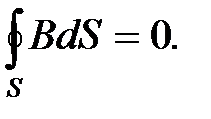
В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.
Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла - интегральная и дифференциальная - эквивалентны. Однако когда имеются поверхности разрыва - поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.
Уравнения Максвелла - наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике.
Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т. е. электрическое и магнитное поля неразрывно связаны друг с другом - они образуют единое электромагнитное поле.
Дата добавления: 2015-08-11; просмотров: 913;
