Второй способ применения метода Гаусса.
Применение метода Гаусса для решения систем линейных уравнений заключается в последовательном исключении неизвестных в уравнениях системы (6.1) с целью приведения ее к треугольному виду:
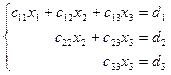 (2)
(2)
При этом допускаются следующие элементарные преобразования системы, приводящие к эквивалентным системам уравнений:
а) перестановка уравнений в системе;
б) умножение обеих частей уравнений на одно и то же число неравное нулю;
в) прибавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на одно и то же число;
г) исключение уравнений вида 0 = 0.
В полученной системе (2) 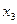 вычисляется из 3-го уравнения и его значение подставляется во 2-е уравнение, затем из 2-го уравнения вычисляется
вычисляется из 3-го уравнения и его значение подставляется во 2-е уравнение, затем из 2-го уравнения вычисляется 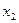 и подставляется вместе с
и подставляется вместе с 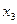 в 1-ое уравнение, после чего из 1-го уравнения вычисляется
в 1-ое уравнение, после чего из 1-го уравнения вычисляется 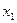 .
.
Пример 2. Дана система линейных уравнений 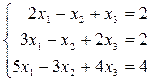 .
.
Решить методом Гаусса.
Решение: Применим метод Гаусса к решению данной системы.
ШАГ 1: умножим 1-ое уравнение системы на 1/ 2, чтобы коэффициент при x1 стал равен единице
ШАГ 2: члены первого уравнения, во-первых, умножим на (-3)
и прибавим к членам второго уравнения, во-вторых, умножим на
(-5) и прибавим к членам третьего уравнения. В результате
получим систему:
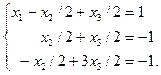
ШАГ 3: к членам третьего уравнения прибавим члены второго уравнения.В результате получим:
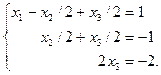
Таким образом, исходная система приведена к эквивалентной системе треугольного вида. Как известно, она имеет единственное решение. Решаем эту систему, начиная с последнего уравнения:
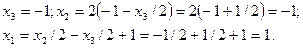
Следовательно, решение системы: 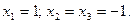
Пример 3. Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом используется сырье трех типов: Sl, S2, S3. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день заданы таблицей:
| Вид сырья | Нормы расхода сырья на одну пару, усл.ед. | Расход сырья на 1 день, | ||
| Сапоги | Кроссовки | Ботинки | ||
| S1 | ||||
| S2 | ||||
| S3 |
Найти ежедневный объем выпуска каждого вида обуви.
Решение. Пусть ежедневно фабрика выпускает х пар сапог, y пар кроссовок и z пар ботинок. Тогда в соответствии с расходом сырья каждого вида имеем систему:
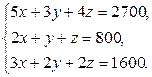
Решая систему любым способом, находим x = 200, y = 300, z = 200, т.е. фабрика выпускает 200 пар сапог, 300 — кроссовок и 200 пар ботинок. Рассмотрим, например, решение системы методом Гаусса:
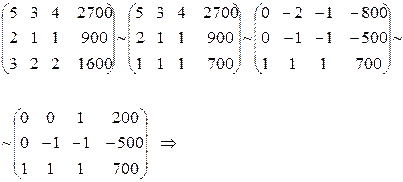
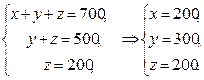
Ответ: ежедневный объем выпуска каждого вида обуви составляет 200 пар сапог, 300 пар кроссовок и 200 пар ботинок.
Дата добавления: 2015-08-21; просмотров: 4226;
