Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы.

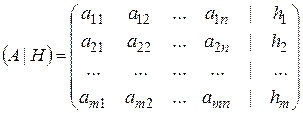- расширенная матрица.

Для определения рангов обеих матриц достаточно привести расширенную матрицу к ступенчатому виду с помощью элементарных преобразований строк и перестановки столбцов (кроме последнего).

Для совместных систем линейных уравнений верны следующие утверждения:

1) Если ранг матрицы совместной системы равен числу переменных, т.е. r(A) = n, то система уравнений (1) имеет единственное решение.

2) Если ранг матрицы совместной системы меньше числа переменных, т.е. r(A) < n, то система (1) неопределенная и имеет бесконечное множество решений.

Схема исследования системы m уравнений с n неизвестными

Система совместная, Система несовместная

если r(A) = r(B) = r. Если r(A) ¹ r(B).

Ответ: нет решений.

Система определена, Система неопределенна,

если r = n. Если r < n.

Ответ: единственное решение. Ответ: бесконечное множество решений.

Пример 2. Дана система линейных уравнений 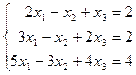. Доказать ее совместность.

Доказательство: Запишем расширенную матрицу системы

и найдем ее ранг. Элемент матрицы 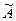, стоящий в левом верхнем углу,отличен от нуля, следовательно среди миноров второго порядка, окаймляющих (включающих в себя) этот элемент, также есть отличные от нуля, например,

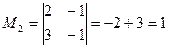, т.е. .

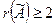Из миноров третьего порядка, окаймляющих 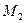, возьмем минор

:

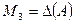Т.к. 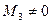то , а т.к. у матрицы 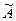миноров 4-го порядка не существует, то . Так как 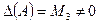, то и 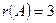. Таким образом, 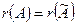, и совместность доказана.

Пример 3. Исследовать систему линейных уравнений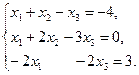

Решение: 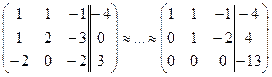, т.к. 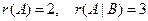, то система несовместна (не имеет решений). В самом деле, последней строке полученной расширенной матрицы соответствует уравнение 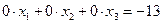, не имеющее решений.

Пример 4. Определить совместность системы уравнений:

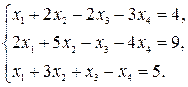
Решение:
Лекция 6. Решение систем линейных уравнений с помощью обратной матрицы.