Системы линейных однородных уравнений. Фундаментальная система решений.

Система mлинейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свобод­ные члены равны нулю. Такая система имеет вид:

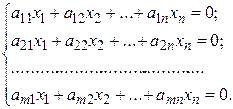(1)

Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (или триви­альное) решение (0; 0; …; 0).

Если в системе (1) m = n , а ее определитель отличен от ну­ля, то такая система имеет только нулевое решение, как это сле­дует из формул Крамера. Ненулевые решения, следо­вательно, возможны лишь для таких систем линейных однород­ных уравнений, в которых число уравнений меньше числа пере­менных, или при их равенстве, когда определитель системы равен нулю.

Иначе: система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при rang(A) < n.

Обозначим решение системы (1) х₁ = k₁, х₂ = k₂,….,x_n = k_n в виде строки е₁ = (k_1,k₂,…,k_n ).

Решения системы линейных однородных уравнений обладают следующими свойствами:

1. Если строка е₁ = (k_1,k₂,…,k_n) — решение системы (1), то
и строка lе₁ = (lk_1, lk₂,…, lk_n )— также решение этой системы.

2. Если строки е₁ = (k_1,k₂,…,k_n ) и е₂ = (l_1,l₂,…,l_n ) —решения системы (1), то при любых с₁ и с₂ их линейная комбинация

c₁ e₁ +c₂ e₂ = (c₁ k₁ +c₂ l₁ ,c₁ k₂ + c₂ l₂ ,…., c₁ k_n +c₂ l_n )

также решение данной системы.

Убедиться в справедливости указанных свойств решений сис­темы линейных однородных уравнений можно непосредственной подстановкой их в уравнения системы.

Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Поэтому представля­ет интерес найти такие линейно независимые решения систе­мы (1), через которые линейно выражались бы все осталь­ные ее решения.

Решения е_1, е₂, …, е_k называются линейно независимыми, если их линейная комбинация l₁е₁ + l₂е₂ +…+ l_ке_к равна нулю, только при условии что l₁ = l₂ =….= l_к = 0.

Определение 2.9. Система линейно независимых решений е_1, е₂, …, е_k называется фундаментальной, если каждое решение системы (1) является линейной комбинацией решений е₁, е₂, …, е_k .

Теорема. Если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений (1) меньше числа пере­менных n, то всякая фундаментальная система решений системы (1) состоит из n – r решений.

Общим решением системы (1) линейных однородных уравнений называется множество всех ее решений, записанных в виде: с₁е₁ + с₂е₂ + … + с _k е _k , где е₁, е₂, … , е_k— любая фундаментальная система решений, с₁, с₂, … , с_k — произвольные числа и k = n – г .

Общее решение неоднородной системы m линейных урав­нений с n переменными равно сумме общего решения соответ­ствующей ей системы однородных линейных уравнений и про­извольного частного решения этой системы.

Пример 1.Решить однородную систему линейных алгебраических уравнений

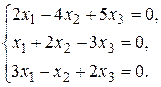
Решение: Определитель системы 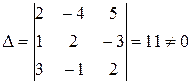, поэтому система имеет единственное нулевое решение: x = y = z = 0.

Пример 2.Найти общее решениесистемы линейных алгебраических уравнений и записать фундаментальную систему решений

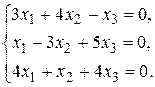
Решение: Определитель системы 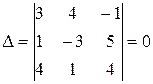, поэтому система имеет бесконечное множество решений. Так как определитель из коэффициентов при неизвестных x₁ и х₂ не равен нулю , то этот минор можно принять за базисный. Поскольку rang A = 2, n = 3, возьмем первые два уравнения системы и найдем ее общее решение.

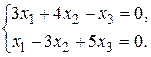
В качестве базисных неизвестных возьмем x₁ и х₂ и переместим члены с х₃ в правые части уравнений:

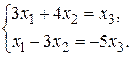
Решая эту систему по формулам Крамера и задав свободной переменной х₃ значение х₃ = c₁ (с₁ – произвольное число), получаем

;

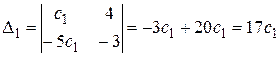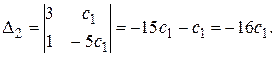
Отсюда находим, что

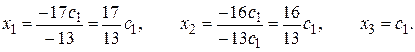
Итак 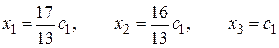- общее решение.

Полагая с₁ = 1, получим частное решение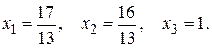

Или в матричном виде 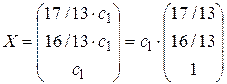. Таким образом, фундаментальная система решений состоит из единственного вектора .

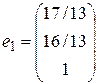Ответ: общее решение ,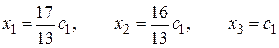

где c₁ - произвольное число. 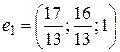- фундаментальная система решений.

Пример 3.Решить однородную систему линейных алгебраических уравнений

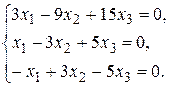
Решение: Определитель системы 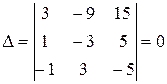, поэтому система имеет бесконечное множество решений. Поскольку все строки матрицы пропорциональны, то rang A = 1. Возьмем любое (например, второе) уравнение системы и найдем ее решение. Так как rang A = 1, n = 3, то базисная переменная одна, остальные две свободные. Фундаментальная система решений состоит из k = n – r = 3 = 1 = 2 решений.

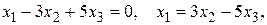полагая х₂ = с₁, х₃ = с₂ получаем решение системы 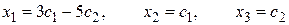, где с₁ и с₂ произвольные числа.

Ответ: общее решение 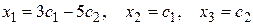, где с₁ и с₂ произвольные числа.