Системы линейных уравнений с квадратной невырожденной матрицей
В случае системы линейных уравнений с квадратной невырожденной матрицей возможно также решение средствами матричного исчисления.
Пусть число уравнений системы равно числу переменных, т.е.
(1) 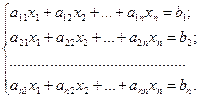
Тогда матрица системы является квадратной, а ее определитель D = |A| называется определителем системы. Запишем систему вида (1) в матричном виде, обозначив матрицу коэффициентов при неизвестных 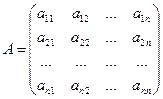 , матрицу столбец свободных членов
, матрицу столбец свободных членов 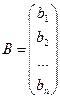 , матрицу столбец неизвестных
, матрицу столбец неизвестных 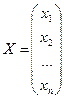 . Умножая матрицы АХ, получаем новую матрицу, элементами которой являются левые части уравнений системы (1). На основании равенства матриц систему (1) можно записать систему (1) в виде АХ=В.
. Умножая матрицы АХ, получаем новую матрицу, элементами которой являются левые части уравнений системы (1). На основании равенства матриц систему (1) можно записать систему (1) в виде АХ=В.
Предположим, что матрица системы А невырожденная, т.е. ее определитель отличен от нуля. Тогда существует обратная матрица А-1. Следовательно решение системы (1) имеет вид Х = А-1 В. Т.е., чтобы найти решение системы, нужно обратную матрицу умножить на столбец свободных членов справа.
Пример 1. Дана система линейных уравнений
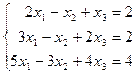 .
.
Доказать ее совместность и решить средствами матричного исчисления.
РЕШЕНИЕ
Докажем совместность. Запишем расширенную матрицу системы

и найдем ее ранг. Элемент матрицы 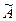 , стоящий в левом верхнем углу,отличен от нуля, следовательно
, стоящий в левом верхнем углу,отличен от нуля, следовательно 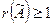 среди миноров второго порядка, окаймляющих (включающих в себя) этот элемент, также есть отличные от нуля, например,
среди миноров второго порядка, окаймляющих (включающих в себя) этот элемент, также есть отличные от нуля, например,
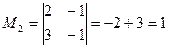 , т.е.
, т.е. 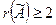 .
.
Из миноров третьего порядка, окаймляющих 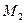 , возьмем минор
, возьмем минор
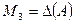 :
:
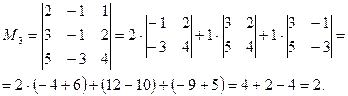
Т.к.  то
то 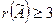 , а т.к. у матрицы
, а т.к. у матрицы 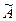 миноров 4-го порядка не существует, то
миноров 4-го порядка не существует, то 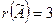 . Так как
. Так как  , то и
, то и 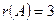 . Таким образом,
. Таким образом,  , и совместность доказана.
, и совместность доказана.
1) Применяем матричный метод к решению системы. Формируем матрицы, состоящие из элементов системы:
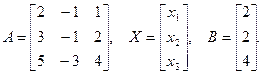
а) Определитель системы 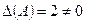 , значит, матричный метод применим.
, значит, матричный метод применим.
б) Запишем систему в матричном виде  :
:
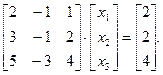
в) Вычисляем алгебраические дополнения  .
.
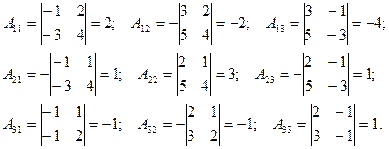
Подставляя найденные значения  в формулу (6.3), получим:
в формулу (6.3), получим:
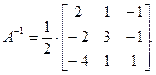
г) воспользуемся формулой (6.4).
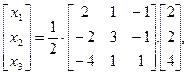
получим:
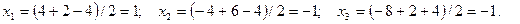
Итак, решение системы: 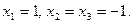
Пример 2. Решить систему уравнений матричным методом.
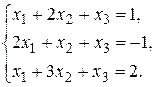
Решение: 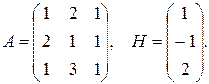
Находим обратную матрицу (самостоятельно)
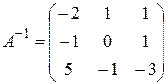 . Следовательно, по формуле Х = А-1×Н, получаем
. Следовательно, по формуле Х = А-1×Н, получаем 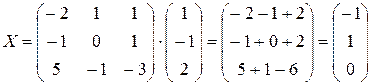 ,
,
т.е. 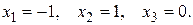
Ответ: 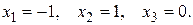
Дата добавления: 2015-08-21; просмотров: 2108;
