Системы линейных неоднородных уравнений

Пусть задана система m линейных уравнений с n неизвестными:

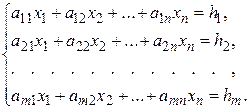(1)

Если 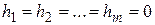, то система (1) называется однородной. Если же хотя бы одно из этих чисел отлично от нуля, то система неоднородная.

Запишем систему вида (1) в матричном виде, обозначив матрицу коэффициентов при неизвестных 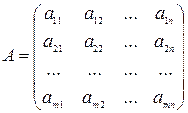, матрицу столбец свободных членов , матрицу столбец неизвестных 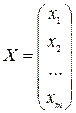. Умножая матрицы АХ, получаем новую матрицу, элементами которой являются левые части уравнений системы (1). На основании равенства матриц систему (1) можно записать систему (1) в виде АХ=В.

Определение 1. Решением системы линейных уравнений вида (1), называется такая совокупность n чисел (k₁, k₂, …, k_n), при подстановке которых каждое уравнение обращается в тождество.

Определение 2. Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.

Определение 3.Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Вопрос о разрешимости системы уравнений в общем виде рассматривается в следующей теореме.

Теорема Кронекера – Капели: