Матричные уравнения.

Матричные уравнения простейшего вида с неизвестной матрицей Х записываются следующим образом АХ=В, ХА=В, АХС=В.

В этих уравнениях А, В, С, Х – матрицы таких размеров, что все используемые операции возможны, и с обеих сторон от знаков равенства находятся матрицы одинаковых размеров.

Если в этих уравнениях матрицы А, В, С – невырожденные, то решения этих уравнений можно записать следующим образом:

1. АХ=В Þ А^-1АХ=А^-1В Þ ЕХ=А^-1В Þ Х=А^-1В.

2. ХА=В Þ ХАА^-1=ВА^-1 Þ ХЕ=ВА^-1 Þ Х=ВА^-1

3. АХС=В Þ А^-1АХСС^-1=А^-1ХС^-1 Þ ЕХЕ=А^-1ХС^-1 Þ Х=А^-1ХС^-1

Пример 1.Решить уравнение АХ=Н

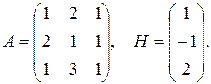
Решение Х=А^-1Н

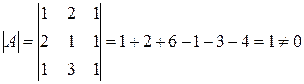. Следовательно матрица невырожденная.

Найдем обратную матрицу. Составим алгебраические дополнения элементов матрицы А.

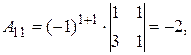
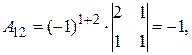
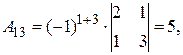
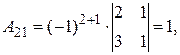
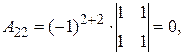
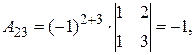
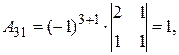
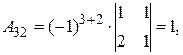
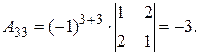
Получаем .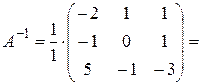

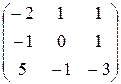Следовательно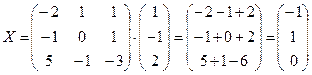

Теория матриц и определителей произвольного порядка строится аналогично изложенной теории матриц и определителей третьего порядка.